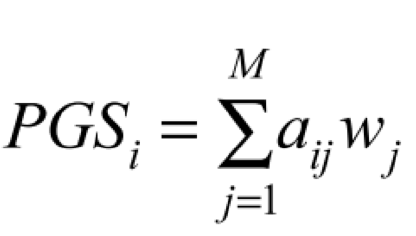Yunye

GWAS多表型分析-MTAG

本文内容：

MTAG简介
核心概念
核心假设
算法简介
特点与不足
使用教程
参考

MTAG简介

MTAG（ multi-trait analysis of GWAS）是一个使用GWAS概括新数据进行多表型联合分析的方法，相比于单表型的GWAS，MTAG可以利用关联表型的信息提升目标表型的检验统计power。

核心概念

MTAG的核心概念是当某个表型的GWAS结果与其他表型的结果存在相关性时，就可以通过整合其他表性的效应量来提高该表型效应量的估计值。

核心假设

对于不同表型，所有的SNP都共享同一个效应量的方差协方差矩阵

MTAG算法简单介绍如下所示：

特点：

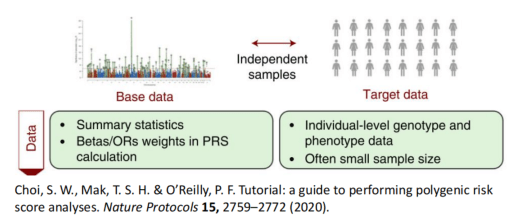
使用GWAS概括性数据，不需要个体基因型信息
所使用的GWAS概括性数据可以有样本重叠，不需要独立样本，因为MTAG会通过二变量LD分数回归来调整样本重叠可能带来的误差。（GWASLab：通过Bivariate LD Score regression估计遗传相关性 genetic correlation）
MTAG可以计算对于特定表型每一个SNP的效应量估计值。
MTAG计算相对高效，因为其每一步都有封闭解。

不足：

MTAG最主要的问题来源于那些与一个表型无关，而与另一个表型存在真实相关的SNP，MTAG对于此类SNP会有估计偏差，对于无关的SNP产生远离0的偏倚，造成假阳性。

使用教程

安装

MTAG是一个基于python的软件，可以从作者的github上下载：

https://github.com/JonJala/mtag

环境要求：

python2.7

numpy (>=1.13.1)
scipy
pandas (>=0.18.1)
argparse
bitarray (for ldsc)
joblib

示例数据下载：

neuroticism 与 subjective well-being gwas的概括性数据：

http://ssgac.org/documents/1_OA2016_hm3samp_NEUR.txt.gz

http://ssgac.org/documents/1_OA2016_hm3samp_SWB.txt.gz

输入格式（GWAS的概括性数据）

snpid    chr    bpos    a1    a2    freq    z    pval    n

snpid，chr，bpos分别为snp的rsID，染色体号，与碱基位置，

a1，a2分别为效应等位（effect allele），与非效应等位

freq为a1的频率

z，pval，n则分别为检验的Z分数，p值，与样本量

（也可以使用beta与se来代替z，-use_beta_se）

MTAG示例代码

python /[path]/mtag.py  \
	--sumstats 1_OA2016_hm3samp_NEUR.txt,1_OA2016_hm3samp_SWB.txt \
	--out ./tutorial_results_1.1NS \
	--n_min 0.0 \
  --stream_stdout

sumstats: 输入的GWAS的概括性数据，使用逗号间隔

out: 输出文件的前缀

n_min：样本量阈值（n低于此阈值的SNP会被舍弃）

stream_stdout : 将log文件实时输出到终端

如果使用东亚的LD分数参考，还需要指定

-ld_ref_panel 这个选项所使用的数据与LDSC相同，可以通过LDSC下载（GWASLab：连锁不平衡分数回归 LD score regression -LDSC）https://alkesgroup.broadinstitute.org/LDSCORE/

输出

总共四组文件，

.log 文件
_sigma_hat.txt 存储估计的残差协方差矩阵
_omega_hat.txt 存储估计的遗传方差矩阵
_trait_1.txt 与_trait_2.txt文件则为MTAG的效应量估计结果

.log 文件：

head -n 20 tutorial_results_1.1NS.log
2021/10/31/10:43:32 PM 
<><><<>><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><>
<>
<> MTAG: Multi-trait Analysis of GWAS 
<> Version: 1.0.8
<> (C) 2017 Omeed Maghzian, Raymond Walters, and Patrick Turley
<> Harvard University Department of Economics / Broad Institute of MIT and Harvard
<> GNU General Public License v3
<><><<>><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><>
<> Note:  It is recommended to run your own QC on the input before using this program. 
<> Software-related correspondence: maghzian@nber.org 
<> All other correspondence: paturley@broadinstitute.org 
<><><<>><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><><>

Calling ./mtag.py \
--stream-stdout  \
--n-min 0.0 \
--sumstats 1_OA2016_hm3samp_NEUR.txt,1_OA2016_hm3samp_SWB.txt \
--out ./tutorial_results_1.1NS

MTAG效应量估计值文件（trait_1）：

head tutorial_results_1.1NS_trait_1.txt
SNP	CHR	BP	A1	A2	Z	N	FRQ	mtag_beta	mtag_se	mtag_z	mtag_pval
rs2736372	8	11106041	T	C	-7.7161416126199995	111111.11111099999	0.4179	-0.032488048690724455	0.004191057650619415	-7.751754186899077	9.063170638233748e-15
rs2060465	8	11162609	T	C	7.69444599845	62500.0	0.6194	0.038971244976047835	0.005364284755639267	7.264947099439278	3.731842884367329e-13
rs10096421	8	10831868	T	G	-7.561098219	111111.11111099999	0.4646	-0.0306226260844897350.004144573386350028	-7.388607518772383	1.483744201034853e-13
rs2409722	8	11039816	T	G	-7.382616018080001	111111.11111099999	0.4627	-0.032187004733709536	0.004145724613962613	-7.763903233057294	8.235474166666265e-15
rs11991118	8	10939273	T	G	7.32202915636	111111.11111099999	0.5056	0.030603923980300953 0.004134432028802615	7.402207550419989	1.339389362466671e-13
rs2736371	8	11105529	A	G	-7.32009158327	62500.0	0.3806	-0.03759068256663257	0.005364284755639268	-7.007585219467501	2.42466338629309e-12
rs2736313	8	11086942	T	C	-7.24228035161	111111.11111099999	0.4646	-0.03068115211425502 0.004144573386350028	-7.402728641577938	1.3341420385130596e-13
rs876954	8	8310923	A	G	-7.15791677597	62500.0	0.4813	-0.03422779585744538	0.005212736369758894 -6.566185862767606	5.162037825451834e-11
rs1533059	8	8684953	A	G	-7.074128564239999	62500.0	0.4478	-0.035027431607855014	0.00523771146606734	-6.687545091932079	2.269452965596589e-11

其中mtag_beta mtag_se mtag_z mtag_pval列为这一个表型mtag计算后的结果。

参考：

Turley, P., Walters, R.K., Maghzian, O.et al.Multi-trait analysis of genome-wide association summary statistics using MTAG.Nat Genet50,229–237 (2018). https://doi.org/10.1038/s41588-017-0009-4

Tutorial 1: The Basics · JonJala/mtag Wiki

使用PLINK检测纯合性片段 ROH（Runs of homozygosity）

本文内容

ROH定义
不同群体ROH的特征
检测ROH的方法
使用PLINK检测ROH

ROH的定义

对于个体，其基因组上的一段区域内所有位点均为纯合的区域，被称为一段纯合性片段 (Runs of homozygosity，ROH). ROH的出现通常是由于个体来自父母双方的单倍体型是相同的，而这个单倍体型又是从过去某个时间点的共同祖先继承而来。ROH的概念不依赖于已知的家系，也不需要一个基线群体。但实际操作中，ROH通常规定有一个基于可用基因型密度的最小的长度，以判别是因为IBD而产生的ROH，或仅仅是概率偶然。

不同群体ROH的特征

不同的群体史会产生不同的长短ROH的分布：

在一个非近交群体（outbred populations ）中，ROH的总数量与总长度与该群体的有效样本量有关，较小的群体趋向于有更多的ROH而较大的群体则趋向于有较少的ROH。

在混合群体（Admixed populations）中，由于该群体的祖先群体共享的祖先成分较远，所以混合群体的ROH通常少于其相应的祖先群体。

在近亲群体（Consanguineous communities）中，与非近交群体相比，会有更长的ROH，这是由于时间上较近的近亲交配，

经历过人口瓶颈（ population bottleneck）的群体则会携带大量的较短的ROH，显示其更深层的父母的亲缘关系。

而经历过人口瓶颈且叠加近亲交配的群体则会有最高程度的ROH。

检测ROH的方法

目前使用最多的检测方法为PLINK中采用的观测法

PLINK采用一个固定大小的滑窗，对每条染色体进行扫描，以寻找连续的纯合SNP。 PLINK首先计算包含某个SNP的完全纯合滑窗的比例，如果该比例超过事先设定好的阈值，那么这个SNP就被认为是在一段ROH中。在每个滑窗中可以指定一定数量的缺失或是杂合的SNP，以包含基因定型错误，失败或是稀有变异等情况。最后，如果在某个片段中连续纯合SNP的数量超过一个数量或距离阈值（SNP数量或是染色体的距离），那么就可以判定这个片段是ROH。

使用PLINK检测ROH

示例代码如下所示：

plink \
        --bfile ${input} \
        --homozyg \
        --homozyg-density 50 \ 一段ROH中每50kb必须有1个SNP
        --homozyg-gap 100 \ 如果连续两个SNP的间隔大于100kb，那么就不能归为同一个ROH
        --homozyg-kb 500 \ 只检测长度大于500kb的ROH
        --homozyg-snp 50 \ 只检测长度超过50个SNP的ROH
        --homozyg-window-het 1 \ ROH滑窗中可以允许有一个SNP位点为杂合
        --homozyg-window-snp 50 \ 滑窗大小为50个SNP
        --homozyg-window-threshold 0.05 \ 包含某个SNP的完全纯合滑窗的比例至少为5%
        --out ${output}

计算完成后会得到 .hom 与.hom.indiv 等文件

.hom 文件包含了每段ROH的具体信息

FID IID PHE CHR SNP1 SNP2 POS1 POS2 KB NSNP DENSITY PHOM PHET
1 1 -9 chr1 rsxxx rsxxx 12345 67891 5.5 123 9.17 0.99 0.07

hom.indiv文件则是包含了对每个个体ROH汇总信息，包括总长度与总个数

FID IID PHE NSEG KB KBAVG
1   1   -9  50   75000  1500

这里的NSEG就是NROH，KB则是SROH

根据上面两个文件就可以做出SROH-NROH图

或是 ROH长度分层的分布图

来判断目标群体的群体特征。

参考：

Ceballos, F. C., Joshi, P. K., Clark, D. W., Ramsay, M. & Wilson, J. F. Runs of homozygosity: windows into population history and trait architecture. Nat. Rev. Genet. 2018 194 19, 220–234 (2018).https://www.nature.com/articles/nrg.2017.109
Identity-by-descent – PLINK 1.9

RaPID高效检测IBD片段 (IBD segments detection)

本文内容:

RaPID简介
RaPID算法
RaPID教程
注意事项
参考

RaPID简介

RaPID是一款用于在基因组数据中检测IBD（identity-by-descent segments）片段的工具，其特点是应用了PBWT（Positional Burrows-Wheeler Transform）算法，能够快速高效地完成检测。BWT被广泛应用于文件压缩与序列比对等领域，序列比对的BWA软件也利用的是这个算法。

IBD回顾：GWASLab：状态同源 / 血缘同源 IBS/ IBD

RaPID算法简介

第一步，通过从每个窗口(wi)内随机取一个变异位点，对输入的定像后的基因型进行多重随机投影。

第二步，对每个投影后的面板使用PBWT（Positional Burrows-Wheeler Transform）算法，找出截断值L以上长度的精确匹配序列。

第三步，收集上一步的精确匹配序列，当某一区域精确匹配序列多于一定数量时，就判定为IBD片段。

图中例子各参数为：长度的截断值为10，窗口大小为5，重复次数为4，成功判定需要的次数为2，不足2次的精确匹配被舍弃

RaPID教程

下载地址：

https://github.com/ZhiGroup/RaPID

RaPID输入文件：

遗产图谱文件格式（tab间隔）：

<site_number> <genetic_location>

每一行包含位点索引以及位点的遗传位置，位点的顺序要与输入VCF文件中位点顺序相同。

该文件的位点顺序应该是单调上升的，且不能有缺失。

RaPID也提供了两个python脚本可以用来对异常图谱进行过滤与插值填充：

对 genetic mapping file 进行过滤

python filter_mapping_file.py <genetic_map> <filtered_map>

对遗传位置进行插值填充, 使位点与输入VCF中位点一一匹配

python interpolate_loci.py <filtered_map> <vcf_input_gzip> <output_map_file>

2. 定相过的VCF文件

参考：GWASLab：Eagle2单倍型定相工具 Haplotype phasing

RaPID_v.1.7 版本具体使用方法

./RaPID_v.1.7 \
	-i <input_file_vcf_compressed> \
	-g <genetic_mapping_file> \
	-d <min_length_in_cM> \
	-o <output_folder> \
	-w <window_size> \
	-r <#runs> \
	-s <#success>

使用作者提供的演示数据：

./RaPID_v.1.7 \
	-i 4k_1e7.vcf.gz \
	-g 4k_1e7_e0.001.g \
	-d 5 \
	-w 250 \
	-r 10 \
	-s 2 \
	-o output_folder

RaPID会将在样本两两之间检测到的所有IBD片段以以下格式输出：

<chr_name> <sample_id1> <sample_id2> <hap_id1> <hap_id2> <starting_pos_genomic> <ending_pos_genomic> <genetic_length> <starting_site> <ending_site>

执行后会得到名为 results.max.gz 的结果

Create sub-samples..
Done!

zcat results.max.gz | head
chr1	0	256	0	0	189	9999752	9.99956	0	94991
chr1	6	1510	1	1	3282417	9616920	6.3345	31000	91249
chr1	18	1801	0	1	189	5186009	5.18582	0	49249
chr1	33	435	0	0	3523968	8873991	5.35002	33250	84249
chr1	42	1854	0	0	1002623	6026274	5.02365	9500	57249
chr1	44	794	1	1	3282417	9797410	6.51499	31000	92999
chr1	51	1394	1	0	3337555	9999752	6.6622	31500	94991
chr1	73	88	1	1	149874	6820265	6.67039	1500	64749
chr1	80	199	0	1	1831845	6974084	5.14224	17500	66249
chr1	82	1849	0	0	3445503	8974078	5.52858	32500	85249

注意事项

如果输入文件的变异密度较低的话，需要相应的减小窗口大小 -w 的值。例如，对于UKBB，位点密度比示例数据中低了80倍，那么窗口小就应相应的从-w 250减小到-w 3.

参考：

Naseri, Ardalan, Xiaoming Liu, Kecong Tang, Shaojie Zhang, and Degui Zhi. “RaPID: ultra-fast, powerful, and accurate detection of segments identical by descent (IBD) in biobank-scale cohorts.” Genome biology 20, no. 1 (2019): 143;
Ultra-fast Identity by Descent Detection in Biobank-Scale Cohorts using Positional Burrows-Wheeler Transform Ardalan Naseri, Xiaoming Liu, Shaojie Zhang, Degui Zhi bioRxiv 103325;

使用UMAP对基因组数据降维，对比PCA

本文内容:
UMAP简介
在群体遗传学中的应用（与PCA的不同）
UMAP使用方法
使用对示例千人基因组数据进行降维
参考

关键词：UMAP, PCA, t-SNE, PCA-UMAP, 基因组降维

UMAP 简介

UMAP（uniform manifold approximation and projection）是近年来新出现的一种相对灵活的非线性降维算法，目前在统计遗传学等领域也有了较为广泛的应用。

UMAP的理论基础基于流形理论（manifold theory）与拓扑分析，

主要基于以下假设：

存在一个数据均一分布的流形。
这个目标流形是局部相连的。
该算法的主要目标是保存此流形的拓扑结构。

总体来看，UMAP利用了局部流形近似，并拼接模糊单纯集合表示（local fuzzy simplicial set representation），以构建高维数据的拓扑表示。在给定低维数据时，UMAP会采取相似的手法构建一个等价的拓扑表示。最后UMAP会对低维空间中数据表示的布局进行最优化，以最小化高维和低维两种拓扑表示之间的交叉熵（cross-entropy）。

算法概览如下：

UMAP与其他降维方法对比：

快，准确：需要降维数据维度增加时，t-SNE计算时间呈指数型增长，umap则线性增长。

在群体遗传学中的应用：

在处理大样本基因组数据时，通常我们会对数据进行降维，以达到数据可视化，并发现存在亲缘关系的样本。

最常用的方法是主成分分析PCA：GWASLab：群体分层与主成分分析教程 Population structure & PCA

UMAP与PCA的不同：

但由于PCA投影找的是最大化方差的方向，通常会忽略掉其他方向的方差，也就是说PCA倾向于发现较大的人群结构，而忽略精细的结构，但UMAP的思路则与PCA不同，如第一节所述，其主要目的是保留其与邻接样本的拓扑结构，也就是更为精细的局部人群结构，而非整体结构。

目前UMAP已经被广泛应用于群体遗传学的研究之中。

下面简单介绍UMAP使用方法：

UMAP （是一个python包），使用方法:

通过pip或conda安装：

pip install umap-learn
#或者
conda install -c conda-forge umap-learn

使用文档详见：https://umap-learn.readthedocs.io/en/latest/parameters.html

一个最简单的示例：

#导入umap包
import umap   

#创建UMAP实例
reducer = umap.UMAP()   

#使用你的数据对该实例进行训练，得到嵌入后的结果
embedding = reducer.fit_transform(your_data)

UMAP() 的主要参数，可参考上述算法概览

n_neighbors ：邻接样本的数量，默认15
min_dist ：控制布局的参数，取值范围0-1，默认0.1
n_components ：维数，默认2

使用基因型数据进行实际演示：

教程改编与数据改编自：

Sakaue, S., Hirata, J., Kanai, M. et al. Dimensionality reduction reveals fine-scale structure in the Japanese population with consequences for polygenic risk prediction. Nat Commun 11, 1569 (2020). https://doi.org/10.1038/s41467-020-15194-z

代码与数据下载：

https://github.com/saorisakaue/Genotype-dimensionality-reduction

数据在umap_data中：1KG.selected.bed/bim/fam

使用软件：

PLINK，python（umap,pandas,matplotlib）

注意：

UMAP只接受完整的数据，对于有缺失的基因型数据要事先对缺失的SNP进行填补以得到完整的数据，填补方法可参考：GWASLab：Eagle2单倍型定相工具 Haplotype phasing
对于PLINK格式的数据，一般需要在LD-pruning 后，转换为 genotype matrix

输入文件预处理：

#如果数据有缺失请先进行填补

#首先进行LD-pruning
GENOTYPE="./data_umap/1KG.selected"

plink \
 --bfile ${GENOTYPE} \
 --indep-pairwise 50 5 0.2 \
 --maf 0.01 \
 --hwe 1E-6 \
 --out ${GENOTYPE}

#对二进制plink文件进行转换,转为0/1/2的文本文件
plink \
 --bfile ${GENOTYPE} \
 --extract ${GENOTYPE}.prune.in \
 --recode A \
 --out ${GENOTYPE}.pruned

# 2) 抽取出 genotype matrix
cat ${GENOTYPE}.pruned.raw | cut -d " " -f7- | awk 'NR>1{print}' > ${GENOTYPE}.pruned.geno.txt

log文件如下：

PLINK v1.90b6.21 64-bit (19 Oct 2020)          www.cog-genomics.org/plink/1.9/
(C) 2005-2020 Shaun Purcell, Christopher Chang   GNU General Public License v3
Logging to ./data_umap/1KG.selected.log.
Options in effect:
  --bfile ./data_umap/1KG.selected
  --hwe 1E-6
  --indep-pairwise 50 5 0.2
  --maf 0.01
  --out ./data_umap/1KG.selected

191875 MB RAM detected; reserving 95937 MB for main workspace.
Allocated 3037 MB successfully, after larger attempt(s) failed.
120489 variants loaded from .bim file.
50 people (25 males, 25 females) loaded from .fam.
Using 1 thread (no multithreaded calculations invoked).
Before main variant filters, 50 founders and 0 nonfounders present.
Calculating allele frequencies... done.
--hwe: 14 variants removed due to Hardy-Weinberg exact test.
861 variants removed due to minor allele threshold(s)
(--maf/--max-maf/--mac/--max-mac).
119614 variants and 50 people pass filters and QC.
Note: No phenotypes present.
Pruned 5127 variants from chromosome 1, leaving 4909.
Pruned 5171 variants from chromosome 2, leaving 4680.
Pruned 4052 variants from chromosome 3, leaving 3919.
Pruned 3398 variants from chromosome 4, leaving 3517.
Pruned 3594 variants from chromosome 5, leaving 3586.
Pruned 4346 variants from chromosome 6, leaving 3628.
Pruned 3298 variants from chromosome 7, leaving 3193.
Pruned 3421 variants from chromosome 8, leaving 3027.
Pruned 2854 variants from chromosome 9, leaving 2895.
Pruned 3445 variants from chromosome 10, leaving 3244.
Pruned 3235 variants from chromosome 11, leaving 3021.
Pruned 2936 variants from chromosome 12, leaving 3020.
Pruned 2281 variants from chromosome 13, leaving 2326.
Pruned 1916 variants from chromosome 14, leaving 2070.
Pruned 1875 variants from chromosome 15, leaving 1943.
Pruned 1848 variants from chromosome 16, leaving 2005.
Pruned 1589 variants from chromosome 17, leaving 1839.
Pruned 1744 variants from chromosome 18, leaving 1925.
Pruned 947 variants from chromosome 19, leaving 1208.
Pruned 1528 variants from chromosome 20, leaving 1620.
Pruned 874 variants from chromosome 21, leaving 887.
Pruned 759 variants from chromosome 22, leaving 914.
Pruning complete.  60238 of 119614 variants removed.
Marker lists written to ./data_umap/1KG.selected.prune.in and
./data_umap/1KG.selected.prune.out .
PLINK v1.90b6.21 64-bit (19 Oct 2020)          www.cog-genomics.org/plink/1.9/
(C) 2005-2020 Shaun Purcell, Christopher Chang   GNU General Public License v3
Logging to ./data_umap/1KG.selected.pruned.log.
Options in effect:
  --bfile ./data_umap/1KG.selected
  --extract ./data_umap/1KG.selected.prune.in
  --out ./data_umap/1KG.selected.pruned
  --recode A

191875 MB RAM detected; reserving 95937 MB for main workspace.
Allocated 3037 MB successfully, after larger attempt(s) failed.
120489 variants loaded from .bim file.
50 people (25 males, 25 females) loaded from .fam.
--extract: 59376 variants remaining.
Using 1 thread (no multithreaded calculations invoked).
Before main variant filters, 50 founders and 0 nonfounders present.
Calculating allele frequencies... done.
59376 variants and 50 people pass filters and QC.
Note: No phenotypes present.
--recode A to ./data_umap/1KG.selected.pruned.raw ... done.

接下来使用umap的默认参数进行降维处理：

import umap

prefix = sys.argv[1]
filename = prefix + ".pruned.geno.txt"
pre_data = pd.read_table(filename, delim_whitespace=True, header=None, low_memory=False)
data = pre_data.dropna(how='any', axis=1)

# UMAP
outfile = prefix + ".umap.txt"
d_embedding = umap.UMAP().fit_transform(data)
pd.DataFrame(d_embedding).to_csv(outfile, sep='\t', header=False, index=False)

查看d_embedding ，基因组数据已经降至2维，结果如下：

array([[ 29.74708  ,   3.0977843],
       [ 29.213293 ,   3.1712177],
       [  8.758959 ,  -1.9003359],
       [  8.377356 ,  -1.4676492],
       [ 29.458044 ,   3.3701472],
       [ 29.87717  ,   3.4556358],
       [ 29.3555   ,   3.8484392],
       [ 28.955818 ,   3.5634878],
       [ 29.105188 ,   2.8024642],
       [ 29.197195 ,   3.7704961],
       [ 29.347229 ,   4.2163496],
       [ 29.865662 ,   3.1569576],
       [  8.503107 ,  -1.3564333],
       [-24.176699 , -14.017474 ],
       [-23.141544 , -13.751009 ],
       [  8.204682 ,  -1.8065634],
       [ 29.94206  ,   2.8537552],
       [-23.501389 , -13.829134 ],
       [ 29.065151 ,   4.255709 ],
       [-23.86171  , -13.711441 ],
       [-23.297297 , -13.290715 ],
       [ 30.9667   , -10.477952 ],
       [-22.91213  , -13.484747 ],
       [-23.249172 , -14.22486  ],
       [-22.951435 , -13.851592 ],
       [ 30.514542 , -11.441013 ],
       [ 30.728407 , -11.229405 ],
       [ 31.13736  , -11.319468 ],
       [ 30.189419 , -10.865067 ],
       [ 30.20413  , -11.283942 ],
       [ 30.89431  , -11.590417 ],
       [ 29.568645 ,   2.9131896],
       [ 29.632095 ,   2.6519256],
       [-23.177608 , -14.538039 ],
       [-23.335829 , -13.95216  ],
       [  8.488959 ,  -2.0645304],
       [  8.731548 ,  -1.8205943],
       [  8.5880165,  -1.6314453],
       [-23.663996 , -13.476801 ],
       [-23.71588  , -14.627886 ],
       [-23.864864 , -14.236027 ],
       [-23.965855 , -14.178329 ],
       [-23.203787 , -14.796338 ],
       [-23.587828 , -14.443732 ],
       [-22.973204 , -14.444413 ],
       [ 30.451714 , -10.90268  ],
       [ 31.011879 , -11.050354 ],
       [ 30.863823 , -10.923892 ],
       [ 30.679998 , -11.574213 ],
       [ 30.77399  , -10.824773 ]], dtype=float32)

绘图后可以看到样本被清楚地分到了4个cluster：

可以自己试着改变UMAP（）的参数，看看有什么变化，这里不过多演示，（下图为UMAP(min_dist=1)的结果）

当然，也可以使用PCA后各个样本主成分PCs进行UMAP （PCA-UMAP）：

PCA方法：GWASLab：群体分层与主成分分析教程 Population structure & PCA

可以参考：Sakaue, S., Hirata, J., Kanai, M. et al. Dimensionality reduction reveals fine-scale structure in the Japanese population with consequences for polygenic risk prediction. Nat Commun 11, 1569

该文章对日本人群结构做了分析，并对比了各种降维方法的结果，强烈推荐。

参考

McInnes, L, Healy, J, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, ArXiv e-prints 1802.03426, 2018

Sakaue, S., Hirata, J., Kanai, M. et al. Dimensionality reduction reveals fine-scale structure in the Japanese population with consequences for polygenic risk prediction. Nat Commun 11, 1569

Diaz-Papkovich, A., Anderson-Trocmé, L. & Gravel, S. A review of UMAP in population genetics. J. Hum. Genet. 66, 85–91 (2021).

https://umap-learn.readthedocs.io

多基因风险分数 PRS( Polygenic risk score)系列之三：使用PRSice计算PRS（C+T方法）

前情回顾：

本文内容：

1 PRSice-2简介与下载
2 PRSice-2教程
3 输入文件
4 C+T 参数
5 PRS计算
6 经验p值计算
7 示例演示
8 参考

PRSice-2简介与下载

PRSice-2是一款方便快捷的PRS计算软件，其主要功能是可以自动化执行一系列PLINK中用于PRS计算的功能，本文将简要讲解PRSice2并演示C+T方法的PRS计算。

PRSice下载链接：

https://www.prsice.info/

演示数据下载（由教程原作者提供，与系列之二PLINK教程中使用的示例数据相同）：

https://drive.google.com/file/d/1x_G0Gxk9jFMY-PMqwtg6-vdEyUPp5p5u/view

PRSice-2教程：

首先，需要的输入文件包括：

1 .base datatset GWAS概括性数据
2 .target dataset 目标数据集
3 .Phenotype files 表型文件
4. covariate files 协变量文件
5 .LD reference (optional: <500 samples) LD参考面板

1.base datatset

通常为GWAS的概括性数据，示例输入文件如下

如果base dataset的格式与示例不同，则可以通过以下选项自行指定

通过列名指定
--snp SNP --chr CHR --bp BP --A1 A1 --A2 A2 --stat OR --pvalue P
或者通过列数指定
--snp 0 --chr 1 --bp 2 --A1 3 --A2 4 --stat 5 --pvalue 7 --index

2.Target Dataset 目标数据集

目标数据集即为目标群体的基因型或填补后的基因型，目前支持PLINK的二进制格式，与BGEN格式

plink文件通过 -target 来指定，输入bed,bim,fam文件的前缀即可

bgen文件还需额外加上 -type bgen 选项

3 & 4 Phenotype & Covariates files

通过–pheno来指定表型文件，该文件是一个tab或space间隔的文本文件，前两列为FID与IID，第三列开始为表型或协变量,例如

FID	IID	Height
HG00096	HG00096	169.132168767547
HG00097	HG00097	171.256258630279
HG00099	HG00099	171.534379938588
HG00101	HG00101	169.850176470551
HG00102	HG00102	172.788360878389
HG00103	HG00103	169.862973824923
HG00105	HG00105	168.939248611414
HG00107	HG00107	168.972346393861
HG00108	HG00108	171.311736719186

如果表性文件中有多列，可以通过–pheno-col来指定表型的列名。

协变量文件格式与表型的一致。

5 LD reference

当样本量小于500时，建议额外指定LD参考面板, 输入格式与上述Target Dataset一致

--ld <LD refernce>

C+T 参数

Clumping

这里的clumping方法与plink的大体一致，可以参考：

SNP的LD剪枝与聚集 LD pruning & clumping

多基因风险分数 PRS( Polygenic risk score)系列之二：使用PLINK计算PRS（C+T方法）

Clumping 参数可以通过 –clump-kb, –clump-r2 与–clump-p 选项来改变。

PRS计算

prsice2提供了多种计算PRS的模型与公式，默认的为计算均值，如下图所述

其他参数

可以指定运行所占用的内存，线程数，以及随机种子

--memory
--thread
--seed

经验p值计算

PRS的计算涉及到参数优化，那么必然会有过拟合的问题。

为了解决这一问题，通常有以下三种方法：

在独立的检验样本中评估
交叉验证
计算经验p值

PRSice2采用了第三种方法，通过permutation 来计算经验p值

PRS计算示例演示：

使用之前下载的示例文件，执行以下命令：

Rscript PRSice.R \
    --prsice PRSice_linux \
    --base Height.QC.gz \
    --target EUR.QC \
    --binary-target F \
    --pheno EUR.height \
    --cov EUR.covariate \
    --base-maf MAF:0.01 \
    --base-info INFO:0.8 \
    --stat OR \
    --or \
    --out EUR

其中

prsice	PRSice_xxx	指定PRSice二进制文件路径 
base	        Height.QC.gz	 输入的base的GWAS summary statistic target	
EUR.QC	指定target的plink文件名的前缀 
binary-target	F	指定表型是否为二进制表型，F为否 
pheno	EUR.height	提供表型文件 
cov	EUR.covariate	        提供协变量文件 
base-maf	MAF:0.01	使用base文件中MAF列来过滤掉maf<0.01的变异 
base-info	INFO:0.8	使用base文件中INFO列来过滤掉info<0.8的变异 stat	
OR	base文件中包含效应量的列名 
or	-	指定效应量的形式为OR 
out	EUR	指定输出前缀为EUR

执行后log文件如下所示：

PRSice 2.3.3 (2020-08-05) 
<https://github.com/choishingwan/PRSice>
(C) 2016-2020 Shing Wan (Sam) Choi and Paul F. O'Reilly
GNU General Public License v3
If you use PRSice in any published work, please cite:
Choi SW, O'Reilly PF.
PRSice-2: Polygenic Risk Score Software for Biobank-Scale Data.
GigaScience 8, no. 7 (July 1, 2019)
2021-09-06 12:47:56
PRSice_linux \
    --a1 A1 \
    --a2 A2 \
    --bar-levels 0.001,0.05,0.1,0.2,0.3,0.4,0.5,1 \
    --base Height.QC.gz \
    --base-info INFO:0.8 \
    --base-maf MAF:0.01 \
    --binary-target F \
    --bp BP \
    --chr CHR \
    --clump-kb 250kb \
    --clump-p 1.000000 \
    --clump-r2 0.100000 \
    --cov EUR.covariate \
    --interval 5e-05 \
    --lower 5e-08 \
    --num-auto 22 \
    --or  \
    --out EUR \
    --pheno EUR.height \
    --pvalue P \
    --seed 3490962723 \
    --snp SNP \
    --stat OR \
    --target EUR.QC \
    --thread 1 \
    --upper 0.5

Initializing Genotype file: EUR.QC (bed) 

Start processing Height.QC 
================================================== 

Base file: Height.QC.gz 
GZ file detected. Header of file is: 
CHR	BP	SNP	A1	A2	N	SE	P	OR	INFO	MAF 

Reading 100.00%
499617 variant(s) observed in base file, with: 
499617 total variant(s) included from base file 

Loading Genotype info from target 
================================================== 

483 people (232 male(s), 251 female(s)) observed 
483 founder(s) included 

489805 variant(s) included 

Phenotype file: EUR.height 
Column Name of Sample ID: FID+IID 
Note: If the phenotype file does not contain a header, the 
column name will be displayed as the Sample ID which is 
expected. 

There are a total of 1 phenotype to process 

Start performing clumping 

Clumping Progress: 100.00%
Number of variant(s) after clumping : 193758 

Processing the 1 th phenotype 

Height is a continuous phenotype 
11 sample(s) without phenotype 
472 sample(s) with valid phenotype 

Processing the covariate file: EUR.covariate 
============================== 

Include Covariates: 
Name	Missing	Number of levels 
Sex	0	- 
PC1	0	- 
PC2	0	- 
PC3	0	- 
PC4	0	- 
PC5	0	- 
PC6	0	- 

After reading the covariate file, 472 sample(s) included in 
the analysis 

Start Processing
Processing 100.00%
There are 1 region(s) with p-value less than 1e-5. Please 
note that these results are inflated due to the overfitting 
inherent in finding the best-fit PRS (but it's still best 
to find the best-fit PRS!). 
You can use the --perm option (see manual) to calculate an 
empirical P-value. 

Begin plotting
Current Rscript version = 2.3.3
Plotting Bar Plot
Plotting the high resolution plot

默认输出结果中有两张图，以及两个文本文件：

第一张为柱状图可以看到不同P值阈值下PRS模型R2的大小：

第二种则是高精度图，表示所有p值阈值的模型拟合：

第一个后缀为prsice的文本文件各个C+T参数的模型的结果：

head EUR.prsice
Pheno	Set	Threshold	R2	P	Coefficient	Standard.Error	Num_SNP
-	Base	5e-08	0.0192512	0.000644758	563.907	164.163	1999
-	Base	5.005e-05	0.0619554	5.24437e-10	3080.12	485.501	7615
-	Base	0.00010005	0.0713244	2.27942e-11	3816.99	557.044	9047
-	Base	0.00015005	0.0785205	2.00391e-12	4362.01	603.601	10014
-	Base	0.00020005	0.0799241	1.24411e-12	4666.13	639.344	10756
-	Base	0.00025005	0.0820088	6.11958e-13	4947.48	668.217	11365
-	Base	0.00030005	0.0818422	6.47686e-13	5146.63	695.905	11884
-	Base	0.00035005	0.0836689	3.47353e-13	5392.8	720.237	12373
-	Base	0.00040005	0.0849879	2.21299e-13	5589.41	739.972	12817

第二个后缀为best的文本文件则为使用最优模型计算得到的target样本的PRS值

head EUR.best
FID IID In_Regression PRS
HG00096 HG00096 Yes -1.90234673e-05
HG00097 HG00097 Yes 1.27505253e-05
HG00099 HG00099 Yes -3.46628033e-06
HG00101 HG00101 Yes 9.02490969e-06
HG00102 HG00102 Yes 1.69546146e-05
HG00103 HG00103 Yes 1.91180157e-05
HG00105 HG00105 Yes 4.62832238e-06
HG00107 HG00107 Yes 7.59715813e-07
HG00108 HG00108 Yes 1.25453063e-05

参考：

https://www.prsice.info/

major/minor/reference/alternative/risk/effect allele 概念解析

这些名词很容易混淆而引起不必要的错误或误解，早期的遗传统计学软件，例如plink并没有很重视allele概念上的明确区分，但近年新出的软件或旧软件的新版本为保证统一性已经开始注意此问题。

本文内容

第一组 频率上的 major 与 minor allele 
第二组 参考基因组的 reference （ref） 与 alternative （alt） allele
第三组 关联检验的 reference （non-risk 或者 non-effect）与 risk/effect allele

首先第一组概念 major 与 minor allele

major allele 与 minor allele 通常针对某一大小确定的特定群体而言，频率最高的allele为该群体的major allele，频率次高的为 minor allele，对于最常见的bi-allelic SNP来说，两个allele频率一高一低，就是这个群体中这个snp的major和minor allele，对于tri- 或者quad-allelic SNP （位点有三种或四种碱基的SNP）而言，minor allele则是频率第二高的那个allele

注意点：

区分major与minor的依据是 某一大小确定特定群体的 allele 频率

plink1.9目前采用的是major与minor allele的概念，软件会自动计算频率，对原始数据进行操作时会自动改变allele的排序，如果你使用plink1.9 的—frq选项计算频率，你会发现输出的文件中是MAF ，minor allele frequency，不会高于0.5。

PLINK1.9中,A1为minor，A2为major allele，所以这里MAF是指A1（minor allele）的频率。。

CHR    SNP    A1   A2          MAF  NCHROBS
1      SNP1    T    C       0.1258    10000
1      SNP2    A    G       0.1258    10000

第二组 reference （ref）与 alternative （alt） allele

reference allele 在这里是指某一参考基因组上该位点的allele，该位点上其他的allele则称为alternative allele。注意，这里reference 与 alternative allele与频率无关，唯一的决定因素是所选的参考基因组。参考基因组上的allele多为major allele，但这只是巧合，不能以此为依据将major和 reference allele划上等号，也有部分reference allele在该群体中为minor allele。

与plink1.9不同，plink2使用的概念则是reference 与 alternative allele，进行操作时不会自动依据频率而改变ref与alt的排序，使用plink2 的—frq选项计算频率，你会发现输出的文件中是alternative allele frequency (不是MAF)，取值范围为[0,1]。

PLINK2中则明确区分了reference 与 alternative allele的概念，例如上述的两个SNP，根据参考基因组对齐后，SNP1在参考基因组中的ref为T，那么alt就为C，这里计算的alt的频率为0.8742，按概念来说在该群体中，SNP1的T为ref allele，但却又是minor allele ，而C为alt，却又是major。对于SNP2来说ref 则为 major，alt 为minor。

#CHROM	ID	REF	ALT	ALT_FREQS	OBS_CT
1	SNP1    	T	C	0.8742	10000
1	SNP2    	G	A	0.1258	10000

小窍门：使用plink2可以将自己手头数据的ref与alt allele与对应参考基因组对齐，示例代码如下：

plink2 \
       --bfile testfile \
       --ref-from-fa -fa hg19.fasta \  从参考基因组的fasta文件来决定plink文件中的ref
       --make-bed \
       --out testfile_fa

第三组 reference 与 risk/effect allele

在这里的概念再次改变，同样的reference allele，在与 risk/effect allele并列时，则指的是GWAS关联检测中的reference allele （non-risk 或者 non-effect），也就是效应量beta（或odds ratio）估计时的对比的参考（reference group），但有的软件也会将 reference allele 作为 effect allele。其概念上与上述ref与alt的组合无关，但为了保持统一性，近年来研究中关联检验的reference 也会与 reference genome保持一致，以避免混淆等。（注意：早期多以minor allele为关联检验的ref allele，这也是容易产生混淆的点）。reference allele的概念非常混乱，辨别时不要拘泥于名称，要关注具体效应量的指代。

risk allele 则很好理解，就是对疾病发生有贡献的那个allele，在复杂疾病的研究中，一般情况下risk allele经常为minor allele，但也会有例外。effect allele的概念也类似，就是我们想要研究其对疾病或表型效应的allele，所以通常是对表型或疾病有贡献的allele，关联检验结果中effect一栏指的就是effect allele的效应。

理解了以上概念后，我们在分辨allele时就能得心应手了。

多基因风险分数 PRS( Polygenic risk score)系列之二：使用PLINK计算PRS（C+T方法）

本文内容

简介
第1步 事先准备
第2步 clumping
第3步 使用PLINK计算PRS
第4步 寻找最佳的P值阈值
参考

简介：

PRS基础回顾 :多基因风险分数 PRS( Polygenic risk score)系列之一：概念入门

PLINK是群体遗传学研究中一款非常强大的软件，尽管PLINK并不是专门为计算PRS而开发，但其内置的功能足以使我们完成C+T （clumping + p value thresholding，也称P + T）计算PRS方法必要的步骤，在初学阶段对于理解PRS计算过程有很大帮助。本文将简要介绍使用PLINK计算PRS的过程（本教程改编自https://choishingwan.github.io/PRS-Tutorial/plink/ ）：

本文所用数据（已经完成QC）：

下载链接，由教程原作者提供：

https://drive.google.com/file/d/1x_G0Gxk9jFMY-PMqwtg6-vdEyUPp5p5u/view

也可以使用自己准备的数据，必要的数据包括

1 target样本的plink文件 (bed,bim,fam)
2 base样本的GWAS概括性数据 
3 target样本的表型数据

第1步事前准备：更新效应量

当表型为二变量表型时，SNP的效应量通常表示为odds ratio（OR），这种情况下计算PRS时要计算乘积，这里为了简化我们将OR转化为beta，就可以只计算加和。

head Height.QC
CHR	BP	SNP	A1	A2	N	SE	P	OR	INFO	MAF
1	756604	rs3131962	A	G	388028	0.00301666	0.483171	0.997886915712650.890557941364774	0.369389592764921
1	768448	rs12562034	A	G	388028	0.00329472	0.834808	1.000687316093530.895893511351165	0.336845754096289
1	779322	rs4040617	G	A	388028	0.00303344	0.42897	0.997603556067569	0.897508290615237	0.377368010940814
1	801536	rs79373928	G	T	388028	0.00841324	0.808999	1.002035699227930.908962856432993	0.483212245374095
1	808631	rs11240779	G	A	388028	0.00242821	0.590265	1.001308325111540.893212523690488	0.450409558999587
1	809876	rs57181708	G	A	388028	0.00336785	0.71475	1.00123165786833	0.923557624081969	0.499743932656759
1	835499	rs4422948	G	A	388028	0.0023758	0.710884	0.999119752645200.906437735120596	0.481016005816168
1	838555	rs4970383	A	C	388028	0.00235773	0.150993	0.996619945289750.907716506801574	0.327164029672754
1	840753	rs4970382	C	T	388028	0.00207377	0.199967	0.997345678956140.914602590137255	0.498936220426316

可以利用简单的R脚本进行转换，在这里我们在文件的最后一列后添加转换后的beta

dat <- read.table(gzfile("Height.QC.gz"), header=T)
dat$BETA <- log(dat$OR)
write.table(dat, "Height.QC.Transformed", quote=F, row.names=F)
q() # exit R

将OR转换成beta后

head Height.QC.Transformed
CHR BP SNP A1 A2 N SE P OR INFO MAF BETA
1 756604 rs3131962 A G 388028 0.00301666 0.483171 0.997886915712657 0.890557941364774 0.369389592764921 -0.00211532000000048
1 768448 rs12562034 A G 388028 0.00329472 0.834808 1.00068731609353 0.895893511351165 0.336845754096289 0.000687079999998082
1 779322 rs4040617 G A 388028 0.00303344 0.42897 0.997603556067569 0.897508290615237 0.377368010940814 -0.00239932000000021
1 801536 rs79373928 G T 388028 0.00841324 0.808999 1.00203569922793 0.908962856432993 0.483212245374095 0.00203362999999797
1 808631 rs11240779 G A 388028 0.00242821 0.590265 1.00130832511154 0.893212523690488 0.450409558999587 0.00130747000000259
1 809876 rs57181708 G A 388028 0.00336785 0.71475 1.00123165786833 0.923557624081969 0.499743932656759 0.00123090000000354
1 835499 rs4422948 G A 388028 0.0023758 0.710884 0.999119752645202 0.906437735120596 0.481016005816168 -0.000880634999999921
1 838555 rs4970383 A C 388028 0.00235773 0.150993 0.996619945289758 0.907716506801574 0.327164029672754 -0.0033857799999997
1 840753 rs4970382 C T 388028 0.00207377 0.199967 0.99734567895614 0.914602590137255 0.498936220426316 -0.00265785000000019

第2步 Clumping （基于P值的LD-pruning）

回顾：SNP的LD剪枝与聚集 LD pruning & clumping

plink \
    --bfile EUR.QC \
    --clump-p1 1 \
    --clump-r2 0.1 \
    --clump-kb 250 \
    --clump Height.QC.Transformed \
    --clump-snp-field SNP \
    --clump-field P \
    --out EUR

其中

–bfile 是输入的PLINK格式文件（target样本）

–clump 则为GWAS的包含P值的概括性数据（base样本）

--clump-p1 1 \
	该选项依据P值，对索引SNP（每个clump中心的SNP）施加过滤，默认值为0.0001
--clump-r2 0.1 \
	与索引SNP的r2大于0.1的位点被归于与索引SNP为同一clump，在计算时去除
--clump-kb 250 \
	进行clumping时只考虑与索引SNP的距离小于250 kb的位点
--clump-snp-field SNP \
	概括性数据文件中变异ID的列名
--clump-field P \
	概括性数据文件中表示P值的列名

详细文档可参考：https://www.cog-genomics.org/plink/1.9/postproc#clump

执行以上命令后我们会得到文件 EUR.clumped，该文件包含clumping后的索引SNP。

head EUR.clumped
CHR    F         SNP         BP        P    TOTAL   NSIG    S05    S01   S001  S0001    SP2
   6    1   rs3134762   31210866  4.52e-165      180     20      0      0      0    160 rs2523898(1),rs13210132(1),rs28732080(1),rs28732081(1),rs28732082(1),rs2517552(1),rs2517546(1),rs2844647(1),rs2517537(1),rs2844645(1),rs2523857(1),rs2517527(1),rs3131788(1),rs3132564(1),rs3130955(1),rs3130544(1),rs2535296(1),rs2517448(1),rs6457327(1),rs28732096(1),rs2233956(1),rs1265048(1),rs3130985(1),rs13201757(1),rs6909321(1),rs3130557(1),rs17196961(1),rs9501055(1),rs13200022(1),rs3130573(1),rs28732101(1),rs1265095(1),rs2233940(1),rs130079(1),rs746647(1),rs2240064(1),rs3131012(1)...

我们可以通过以下代码提取这些SNP的id, 用于下一步计算

awk 'NR!=1{print $3}' EUR.clumped > EUR.valid.snp

注意：

这里的r2计算是基于最大似然单倍型频率估计的，如果你的target样本比较少（<500），那么计算LD的r2时最好使用千人基因组项目中相应群体的数据。

第3步计算 PRS

plink提供了—score选项，是我们可以方便的计算PRS

需要以下输入文件：

base样本的GWAS概括性数据文件 Height.QC.Transformed
一个包含SNP ID与相应P值的文件
使用awk命令从Height.QC.Transformed中提取SNPID与P值即可
awk ‘{print $3,$8}’ Height.QC.Transformed > SNP.pvalue

在这里我们计算多个P值范围内SNP的PRS

echo "0.001 0 0.001" > range_list 
echo "0.05 0 0.05" >> range_list
echo "0.1 0 0.1" >> range_list
echo "0.2 0 0.2" >> range_list
echo "0.3 0 0.3" >> range_list
echo "0.4 0 0.4" >> range_list
echo "0.5 0 0.5" >> range_list

上述范围的三个数字分别为，名称，范围的下限，范围的上限

例如0.001 0 0.001 ，名称为0.001的这个范围，下限为0，上限为0.0001

下面开始计算，PLINK代码如下

plink \
    --bfile EUR.QC \
    --score Height.QC.Transformed 3 4 12 header \
    --q-score-range range_list SNP.pvalue \
    --extract EUR.valid.snp \
    --out EUR

其中 –q-score-range 即为包含P值范围的文件与一个包含SNP ID与相应P值的文件

–score 为计算分数的选项，3, 4，12 分别表示SNP ID，allele code与beta 分别在文件的第 3， 4， 12列， header表示输入文件有表头。

当然在计算时也可以加入协变量，例如PC等，这里就略过

执行后输出对应上述7个范围的PRS的文件：

EUR.0.5.profile
EUR.0.4.profile
EUR.0.3.profile
EUR.0.2.profile
EUR.0.1.profile
EUR.0.05.profile
EUR.0.001.profile

head EUR.0.001.profile
FID       IID  PHENO    CNT   CNT2    SCORE
  HG00096   HG00096     -9  32678   6894 -4.41148e-05
  HG00097   HG00097     -9  32678   6921 5.71558e-05
  HG00099   HG00099     -9  32678   6759 7.23017e-07
  HG00101   HG00101     -9  32678   6875 3.48096e-05
  HG00102   HG00102     -9  32678   6966 4.68491e-05
  HG00103   HG00103     -9  32678   6763 8.78172e-05
  HG00105   HG00105     -9  32678   6960 4.39891e-05
  HG00107   HG00107     -9  32678   6835 2.45655e-05
  HG00108   HG00108     -9  32678   6884 7.68976e-05

第4步寻找 best-fit PRS

通常情况下，事先我们并不知道最优的P值阈值，所以在计算完成多组PRS后，为了找到最适阈值，需要对PRS进行回归分析，然后选取能够解释最多表型方差的P值阈值。

示例R代码如下 bestfit.R

p.threshold <- c(0.001,0.05,0.1,0.2,0.3,0.4,0.5)
# Read in the phenotype file 
phenotype <- read.table("EUR.height", header=T)
# Read in the PCs
pcs <- read.table("EUR.eigenvec", header=F)
# The default output from plink does not include a header
# To make things simple, we will add the appropriate headers
# (1:6 because there are 6 PCs)
colnames(pcs) <- c("FID", "IID", paste0("PC",1:6)) 
# Read in the covariates (here, it is sex)
covariate <- read.table("EUR.cov", header=T)
# Now merge the files
pheno <- merge(merge(phenotype, covariate, by=c("FID", "IID")), pcs, by=c("FID","IID"))
# We can then calculate the null model (model with PRS) using a linear regression 
# (as height is quantitative)
null.model <- lm(Height~., data=pheno[,!colnames(pheno)%in%c("FID","IID")])
# And the R2 of the null model is 
null.r2 <- summary(null.model)$r.squared
prs.result <- NULL
for(i in p.threshold){
    # Go through each p-value threshold
    prs <- read.table(paste0("EUR.",i,".profile"), header=T)
    # Merge the prs with the phenotype matrix
    # We only want the FID, IID and PRS from the PRS file, therefore we only select the 
    # relevant columns
    pheno.prs <- merge(pheno, prs[,c("FID","IID", "SCORE")], by=c("FID", "IID"))
    # Now perform a linear regression on Height with PRS and the covariates
    # ignoring the FID and IID from our model
    model <- lm(Height~., data=pheno.prs[,!colnames(pheno.prs)%in%c("FID","IID")])
    # model R2 is obtained as 
    model.r2 <- summary(model)$r.squared
    # R2 of PRS is simply calculated as the model R2 minus the null R2
    prs.r2 <- model.r2-null.r2
    # We can also obtain the coeffcient and p-value of association of PRS as follow
    prs.coef <- summary(model)$coeff["SCORE",]
    prs.beta <- as.numeric(prs.coef[1])
    prs.se <- as.numeric(prs.coef[2])
    prs.p <- as.numeric(prs.coef[4])
    # We can then store the results
    prs.result <- rbind(prs.result, data.frame(Threshold=i, R2=prs.r2, P=prs.p, BETA=prs.beta,SE=prs.se))
}
# Best result is:
prs.result[which.max(prs.result$R2),]
q() # exit R

执行后就可以看到本次PRS计算中，最优的阈值为0.3

Rscript bestfit.R 
  Threshold        R2            P     BETA       SE
5       0.3 0.1638468 1.025827e-25 47343.32 4248.152

参考：

Basic Tutorial for Polygenic Risk Score Analyses

HLA系统命名规则

本文内容：

背景
HLA简介
命名规则 Nomenclature
一些特殊标记
HLA分型的解析度 Resolution
参考

背景

WHO的 Nomenclature Committee for Factors of the HLA System 为了区分编码HLA分子的HLA等位基因，于1987年开始施行4位数字的命名方法。后在2002年，由于4位数字的命名法已经不再适应该领域的快速发展，遂将HLA-A*02 群改为 A*92，将HLA-B15改为B95进行管理。但近年随着等位基因数的不断增加，其他的抗原群也难以在现行命名规则下管理。于是在2010年，发布了现行的HLA等位基因命名规则。这次变更后，使用冒号“：”分隔表示不同HLA等位基因的4个数字区域，并取消了固定位数的限制。

已发现的HLA等位基因数量逐年增加：

HLA基础：推荐 https://zhuanlan.zhihu.com/p/382011751 ，简单易懂

命名规则如下图所示：

HLA为前缀，A表示基因，使用星号*与4个数字区域进行分割。

被冒号“：”分隔的四个数字区域分别标示以下内容：

・第 1 区域：相关联的血清学HLA分型，或是该等位基因所属的等位基因组（例：A*02，A*03，A*11，C*03 等）
・第 2 区域：同一血清学 HLA 型或是等位基因组内，伴随氨基酸变异的等位基因（亚型）（例：A*02:02，A*02:04，A*02:07等）

・第 3 区域：不伴随氨基酸变异的等位基因（同义置换：synonymous DNA substitution）（例：A*02:01:02，A*02:01:03，A*02:01:04 等）
・第 4 区域：非编码区域伴随碱基置换的等位基因（例：A*02:01:01:01，A*02:01:01:02L，A*02:01:01:03 等）

一些特殊标记：

存在两种以上等位基因无法判定时使用 / 分隔，例如：HLA-DRB1*15/16
无法判定的等位基因过多时，使用+表示省略，例如：HLA-DRB1*15:01/16:01/+
表示肽链结合区（HLA class I：exon2 和3，HLA class II ：exon2）的不确定性时，氨基酸序列（P），或是碱基序列（G）一致的等位基因，在末尾添加P或G表示。例如：A02:01:01:01/02:01:01:02L/02:01:01:03/02:01:02/02:01:03/02:01:04/02:01:05/02:01:06/02:01:07/02:01:08/02:01:09/02:01:10/02:01:11/02:01:12/02:01:13/02:01:14/02:01:15/02:01:17/02:01:18/02:01:19/02:01:21/02:01:22/02:09/02:66/02:75/02:89/02:97/02:132/02:134/02:140 可以表示为 A02:01P
N: Null alleles 不表达的等位基因
L：Low cell surface expression 在细胞表面低表达
S：Soluble 该等位基因表达的蛋白可溶
C：Cytoplasm 表达的蛋白在细胞质
A：Aberrant 不确定是否表达
Q：Questionable 可疑的，该等位基因中的变异会影响其他等位基因的正常表达

HLA分型的解析度：

可以分为

1.低解析度（low resolution）：至精确到第一个数字区域，例如：A*02。

2.高解析度（high resolution）：通常精确到表达同一蛋白的一组等位基因，也就是至少包含两个数字区域，例如：A*02:07。

3.等位解析度（Allelic resolution）：精确到该等位基因的所有位数，例如A*01:01:01:01。

4.其他解析度，例如 G-group：精确到G组（见上述特殊标3的G标记），例如：A*02:01:01G

参考：

http://hla.alleles.org/nomenclature/stats.html

Nunes E, Heslop H, Fernandez-Vina M, Taves C, Wagenknecht DR, Eisenbrey AB, Fischer G, Poulton K, Wacker K, Hurley CK, Noreen H, Sacchi N; Harmonization of Histocompatibility Typing Terms Working Group. Definitions of histocompatibility typing terms: Harmonization of Histocompatibility Typing Terms Working Group. Hum Immunol. 2011 Dec;72(12):1214-6. doi: 10.1016/j.humimm.2011.06.002. Epub 2011 Jun 15. PMID: 21723898.

多基因风险分数 PRS( Polygenic risk score)系列之一：概念入门

本文将讲解多基因风险分数PRS（Polygenic risk score，或称PGS）的相关基础概念，

PRS的背景
PRS的概念与定义
PRS的一般性质
构建PRS的注意事项
PRS的验证与预测
相关软件
参考

1. PRS的背景与概念

（首先复习：遗传结构 Genetic architecture ）

一般情况下，对于单基因疾病（孟德尔遗传病）来说，只有单个或少数基因对表型有很大的影响，与之相对，对于复杂疾病来，通常有大量的遗传位点对表型有较小的影响，目前GWAS研究多基于此类无限小的假设（详见：解释复杂疾病的四种主流模型 CDCV/RAME/infinitesimal/Broad-sense-heritability ），这种情况下单个变异不足以用来评估个体对某一复杂疾病的风险，所以为了找到一个能够评估个体疾病风险的值，PRS （多基因风险评分）就应运而生，PRS的概念简单说就是，总和多个遗传变异与表型关系的数值。

2. PRS的一般定义

PRS (polygenic risk score，多基因风险分数) , 对于非疾病的表型也称为 PGS (polygenic score)

实际研究中，PGS 的数学上的定义一般如下所示：

PGS是基因组上与表型相关等位基因的加权线性组合（权重通常为GWAS中估计的效应量）。

其中： i 表示第i个个体, j 为第j个SNP, wj为该SNP的权重,a则为第i个个体第j个SNP的等位基因拷贝数

这里要注意：

通常PGS假设潜在的模型是加性模型（additive model）。

上述式子是一个概念性的定义式，实际操作中还需要进行额外操作。

3 PRS的一般性质

PRS可以被认为是多个独立的遗传信号的总和，那么根据中心极限定理，PRS也近似服从正态分布。

4.构建PRS的注意事项

4.1 GWAS discovery阶段的样本量要足够大

大的样本量：

有助于减少采样误差（sampling error），
有助于获得更精准的效应量估计值
同时也有助于发现效应量较小的SNP （回忆 missing heritability 遗传力 Heritability 与 Missing heritability）

好在从GWAS Diversity Monitor （https://gwasdiversitymonitor.com/）上可以看到，GWAS的样本量是在逐年上升的，目前规模最大的GWAS的样本量已经达到了三百万的级别，这将在未来有效促进PRS的构建。

4.2 选择纳入计算的SNP

这包含了两方面因素，1是纳入计算的SNP的数量如何决定，2是对于纳入的SNP如何施加权重。通常情况下这两方面的选择取决于研究的表型，与应用的类型。

目前主要的方法包括：

GWAS中对SNP的检验通常是逐个进行的，由于LD的存在，这会使得SNP的效应估计值有偏差，继而导致PRS出现偏倚。为了减弱这种偏差目前有两种主流方法：

4.2.1 p值 clumping + thresholding法 (P+T 或 C+T) :

一种常用的方法就是在PRS的计算中只纳入一部分SNP，也就是先进行clumping(基于p值的pruning) （详见：SNP的LD剪枝与聚集 LD pruning & clumping），筛出各个loci里p值最低的SNP，然后再基于p值的某个阈值，选择纳入的SNP。

4.2.2 beta 缩减法

与第一种纳入部分SNP的思路不同，第二种方法是纳入所有的SNP，但在计算时会基于LD信息调整SNP的权重，例如LASSO回归（lassosum），与一些基于贝叶斯方法的算法（LDpred等）。

5 PRS的验证与预测

5.1 要注意的是，在PRS研究中要使用独立的样本，也就是在GWAS discovery阶段使用的样本与PRS的目标样本之间不应该有重复。这主要是为了避免overfitting 过拟合的问题。只有当样本量足够大时，才可以使用同一样本。

5.2 目标样本应当为同一族裔。

由于不同族裔之间，MAF，局部LD等等的不同，PRS的泛用性较差。例如由BBJ计算而得的二型糖尿病PRS模型，应用到UKBB的人群中时，预测的r2明显降低。

5.3 提升PRS跨族裔泛用性

值得注意的是，目前也有研究致力于提升PRS在不同族裔间的泛用性。例如Amariuta等就基于转录因子介导的细胞特异的调节的位点的功能注释（Functional annotations marking the precise location of TF-mediated cell-type-specific regulation ）来降低群体特异的LD结构（population-specific LD），以提升PRS在不同族裔间的准确度。

6 目前使用较多的PRS软件包括：

PLINK 多基因风险分数 PRS( Polygenic risk score)系列之二：使用PLINK计算PRS（C+T方法）

PRSice 多基因风险分数 PRS( Polygenic risk score)系列之三：使用PRSice计算PRS（C+T方法）

LDpred 1/ 2

PRS-CS 多基因风险分数 PRS( Polygenic risk score)系列之五：使用PRS-CS计算PRS（beta-shrinkage方法）

Lassosum

等等，我会在后续的文章中介绍具体使用方法。

其他PRS相关文章：

7 参考：

Choi, S. W., Mak, T. S. H. & O’Reilly, P. F. Tutorial: a guide to performing polygenic risk score analyses. Nature Protocols 15, 2759–2772 (2020).

McCarthy, M., Abecasis, G., Cardon, L. et al. Genome-wide association studies for complex traits: consensus, uncertainty and challenges. Nat Rev Genet 9, 356–369 (2008).

Amariuta, T. et al. Improving the trans-ancestry portability of polygenic risk scores by prioritizing variants in predicted cell-typespecific regulatory elements. Nature Genetics 52, 1346–1354 (2020).

使用GWAS概括性数据进行条件分析 GCTA – COJO

GCTA-COJO: multi-SNP-based conditional & joint association analysis using GWAS summary data

本文内容：

背景介绍
GCTA-COJO使用方法
参考样本的选择
参考

背景介绍：

通常情况下GWAS或是meta分析检验的是基于单个SNP模型的相关，所估计的效应量为被检验SNP的边际效应，但相比于多SNP模型的联合效应，单个SNP模型的边际效应并没有考虑该SNP与周围SNP的LD。

这会带来两个问题：

如果两个SNP成负相关，那么这两个SNP的效应都会被减弱。
如果两个SNP都达到了显著的阈值，事后很难通过LD来确定这两个SNP的相关的程度。

如果我们有原始样本层面的基因型，以及单SNP检验后的概括性数据，就可以在没有表型数据的情况下，将边缘效应转化为联合效应。

但一般情况下，对于一个包含很多队列的meta分析，我们无法获取个体的基因型数据，所以不能计算X′X（转化为联合效应时必须的步骤），但X′X本质上是一个SNP基因型的协方差矩阵，我们可以通过1.meta-analysis的基因型频率，与2.从可以获得基因型的参考样本计算而得的SNP之间的LD，来进行估计。这样的基于meta分析的基因频率与参考队列的LD的估计过程也可以用在相应的条件分析之中。（详细推导过程见原文）

使用方法：

COJO内置于GCTA软件中：

输入文件为

来自meta分析的概括性数据 summary-level statistics from a meta-analysis GWAS
参考样本的基因组文件 plink格式

-cojo-file [test.ma](<http://test.ma/>) 用于指定概括性数据：

概括性数据输入文件格式如下所示，

SNP A1 A2 freq b se p N 
rs1001 A G 0.8493 0.0024 0.0055 0.6653 129850 
rs1002 C G 0.0306 0.0034 0.0115 0.7659 129799 
rs1003 A C 0.5128 0.0045 0.0038 0.2319 129830
...

需要包含，各列需要按次顺序排列，列名则没有要求

1.SNP的ID，
2.效应等位A1，      #注意 A1,A2不能颠倒
3.参考等位A2，
4.效应等位的频率，   #也就是A1的频率
5.效应的大小，
6.标准差，
7.p值，
8.以及样本大小

注意

1.对于病例对照研究，效应大小应当是 log(odds ratio),以及其相对应的标准差。

即使你的研究对象只是一部分SNP，在准备输入文件时，也要准备所有SNP的概括性数据，主要原因是GCTA-COJO需要所有SNP的概括性数据来计算表型方差。可以使用--extract选项来限制COJO分析的区域。

COJO分析中可用的选项：

--cojo-slct

通过逐步法筛选出独立关联的SNP。结果将保存在*.jma文件中，还会有一个额外的文件*.jma.ldr保存SNP两两间的LD。

--cojo-top-SNPs 10

通过逐步法筛选出指定数量的独立关联的SNP，不设P值得阈值，找到指定数量的SNP为止。输出文件同--cojo-slct

--cojo-joint

不进行模型筛选，直接估计所有纳入的SNP的联合效应。输出文件同上。

--cojo-cond cond.snplist

校正给定列表中的SNP后进行关联分析。结果将保存在*.cma文件中。

其中cond.snplist的格式如下所示：

rs1001
rs1002
...

--cojo-p 5e-8

基因组范围显著的阈值，默认为 5e-8 。当使用–cojo-slct时，该选项才有效。

-cojo-wind 10000

当两个SNP的距离超过指定值时，认为其为连锁平衡的。默认值为10000 Kb (i.e. 10 Mb)

-cojo-collinear 0.9

模型选择时，程序会检查SNP之间的共线性问题，如果某一SNP在回归中的R2大于阈值，那么该SNP将不会被选择。默认值为0.9 。

-diff-freq 0.2

检查GWAS概括性数据中频率与参考样本中频率的差值，差值过大的SNP会被去除。默认值为0.2.

-cojo-gc

选择后p值会进行基因组控制。 e.g. –cojo-gc 1.05.

COJO分析的使用例：

# Select multiple associated SNPs through a stepwise selection procedure
gcta64  --bfile test  --chr 1 --maf 0.01 --cojo-file test.ma --cojo-slct --out test_chr1

# Select a fixed number of of top associated SNPs through a stepwise selection procedure
gcta64  --bfile test  --chr 1 --maf 0.01 --cojo-file test.ma --cojo-top-SNPs 10 --out test_chr1

# Estimate the joint effects of a subset of SNPs (given in the file test.snplist) without model selection
gcta64  --bfile test  --chr 1 --extract test.snplist  --cojo-file test.ma --cojo-joint --out test_chr1

# Perform single-SNP association analyses conditional on a set of SNPs (given in the file cond.snplist) without model selection
gcta64  --bfile test  --chr 1 --maf 0.01 --cojo-file test.ma --cojo-cond cond.snplist --out test_chr1

输出文件格式

结尾为.jma的文件（使用-cojo-slct 或 –cojo-joint时的输出）

Chr SNP bp freq refA b se p n freq_geno bJ bJ_se pJ LD_r
1 rs2001 172585028 0.6105 A 0.0377 0.0042 6.38e-19 121056 0.614 0.0379 0.0042 1.74e-19 -0.345
1 rs2002 174763990 0.4294 C 0.0287 0.0041 3.65e-12 124061 0.418 0.0289 0.0041 1.58e-12 0.012
1 rs2003 196696685 0.5863 T 0.0237 0.0042 1.38e-08 116314 0.589 0.0237 0.0042 1.67e-08 0.0 
...

输出文件的列依次是染色体号，SNP ID，位置，效应等位的频率，效应量大小，标准差，原始P值，估计的有效样本量，参考样本中的频率，joint analysis中该SNP的效应量大小，标准差，P值，以及列表中第i个SNP与第i+1个SNP的LD。

LD矩阵（使用-cojo-slct 或 –cojo-joint时的输出）

存储于后缀为jma.ldr的文件中

SNP rs2001 rs2002 rs2003 ...
rs2001 1 0.0525 -0.0672 ...
rs2002 0.0525 1 0.0045 ...
rs2003 -0.0672 0.0045 1 ...
...

结尾为.cma的文件（使用–cojo-cond选项会生成）

Chr SNP bp freq refA b se p n freq_geno bC bC_se pC
1 rs2001 172585028 0.6105 A 0.0377 0.0042 6.38e-19 121056 0.614 0.0379 0.0042 1.74e-19
1 rs2002 174763990 0.4294 C 0.0287 0.0041 3.65e-12 124061 0.418 0.0289 0.0041 1.58e-12
1 rs2003 196696685 0.5863 T 0.0237 0.0042 1.38e-08 116314 0.589 0.0237 0.0042 1.67e-08
...

GCTA-COJO 分析中参考样本的选择（重要！）

如果你的概括性数据来自单一的GWAS，那么最好的参考样本就是这个GWAS中的样本。
当概括性数据来自Meta分析，个体的基因型无法获取时，可以使用一个样本量较大队列的数据。例如，Wood et al. 2014 Nat Genet 使用了ARIC cohort (data available from dbGaP)
建议使用样本量大于4000的参考样本
不建议使用 HapMap 或 1000G 的参考样本，因为其样本量太小。

实际使用中可以使用填补后的基因型数据来估计LD，例如可以从BBJ中随机抽取20000个无关联的个体，提取其填补后的基因型作为EAS群体的参考面板。

参考：

Conditional and joint analysis method: Yang et al. (2012) Conditional and joint multiple-SNP analysis of GWAS summary statistics identifies additional variants influencing complex traits. Nat Genet 44(4):369-375. [PubMed ID: 22426310]

GCTA software: Yang J, Lee SH, Goddard ME and Visscher PM. GCTA: a tool for Genome-wide Complex Trait Analysis. Am J Hum Genet. 2011 Jan 88(1): 76-82. [PubMed ID: 21167468]