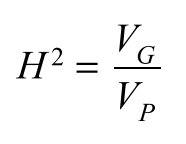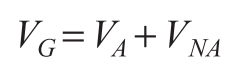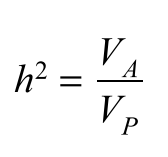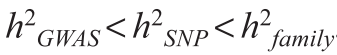00 群体遗传学基础 population genetics – 第 2 页 – GWASLab

易感性-阈值模型 Genetic liability, Threshold model

易感性-阈值模型是遗传流行病学中重要的理论模型之一。

Liability 易感性

易感性是 遗传因素 与 环境因素 对某多因子疾病的效应的总称。因为易感性是一个隐变量（latent variable），实际上很难直接测量某个特定个体的易感性，但我们可以通过某群体中发病个体数量来估计该群体对于疾病的易感性。

Threshold Model 阈值模型

易感性-阈值模型（liability -threshold model）是我们用来分析非孟德尔遗传的（non-Mendelian）分类（categorical）表型（例如二分类表型 binary traits）的基本模型之一，如下图所示，通常我们认为易感性服从一个N(0,1)的正态分布。当某个个体的集聚的易感性超过了阈值T时就会发病，阴影区域的面积表述了在这个群体中该疾病的流行率（prevalence）。

对于某个疾病可以有多个阈值，分别对应疾病的不同严重程度。

参考：

https://onlinelibrary.wiley.com/doi/full/10.1002/0470011815.b2a05036

遗传力 Heritability 与 Missing heritability

本文关键词： Heritability， h2, family heritability , SNP heritability, GWAS heritability , Missing heritability

遗传力的基础概念

遗传力（Heritability）是我们理解遗传与环境因素对性状影响的基础，定义为遗传方差占性状方差（总方差）的比值，可以理解为遗传因素对性状的影响，数学上以h2表示。

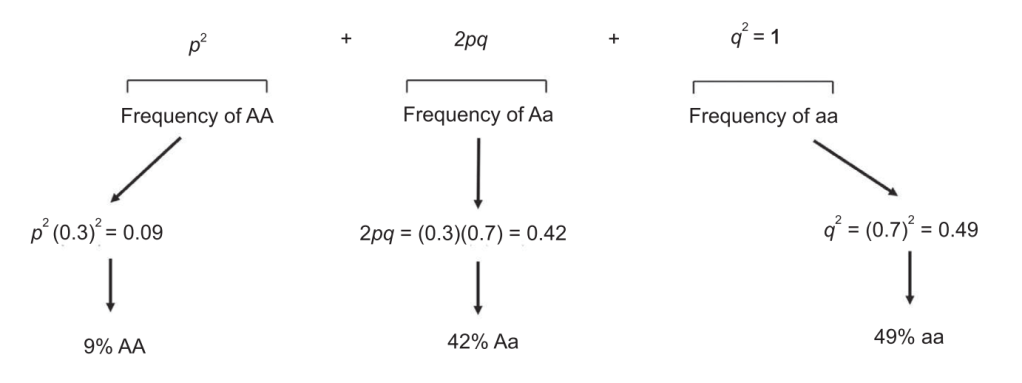
通常根据对遗传方差的定义而分为广义与狭义遗传力：

广义遗传力 broad-sense heritability ：

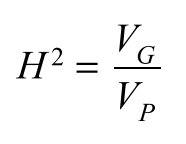其中VP = VG + VE, VP为性状方差，VE为环境方差（也包括测量误差等），而分子的VG为遗传方差。

遗传方差VG也可进一步细分为

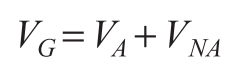VA是加性遗传效应的方差，VNA是非加性遗传效应的方差（上位与显性遗传效应）

加性遗传效应是指当两个或多个基因对于某一性状，或是单个基因的不同等位基因对于某一性状的整体作用，等于它们单独作用之和。

非加性遗传效应则包括上位与显性遗传效应。

因为对于绝大多数复杂性状，很少有证据证明有非加性遗传效应存在，所以我们目前聚焦于主要考虑加性遗传效应的狭义遗传力，

狭义遗传力 narrow-sense heritability ：

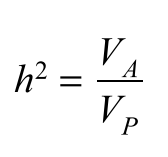
遗传力的估计

我们有多种方法可以估计遗传力h2的大小，目前主要的方法有三种，通过双胞胎研究，SNP或是GWAS来估计。

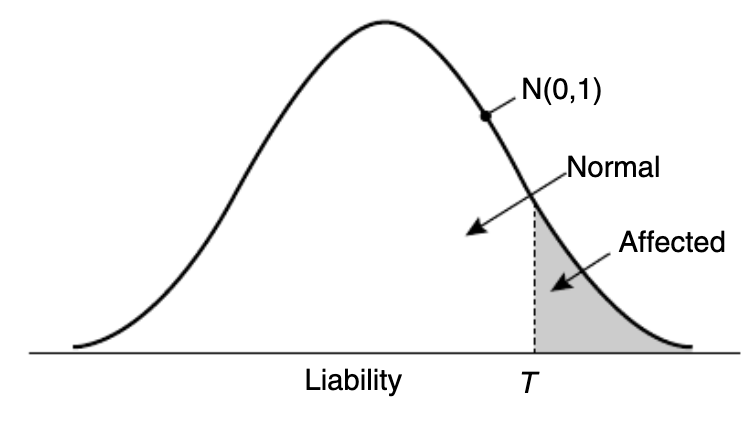
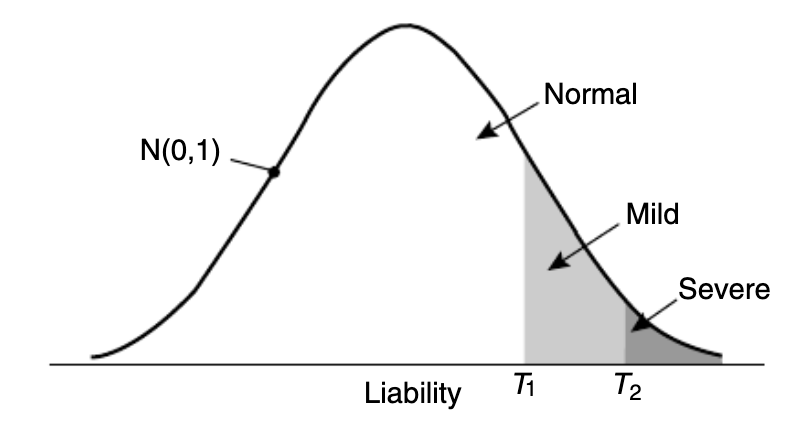
h2 family ：双胞胎研究，通过比较同卵与异卵双胞胎的相似性，计算得到h2，通常为这三种中最高。

h2 SNP ：GWAS研究所用chip上所有variants共同解释的方差与性状方差的比值，比 h2 family 低，但会显著高于h2 GWAS。可以使用GCTA的GREML模型来估计。（使用GCTA （GREML）来估计SNP-遗传力 SNP Heritability ）

h2 GWAS ：仅由GWAS所发现的某疾病相关variants解释的方差与性状方差的比值，三者中最低。

一般情况下，三者的关系：

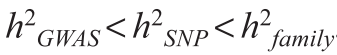
更直观的关系如下图所示：

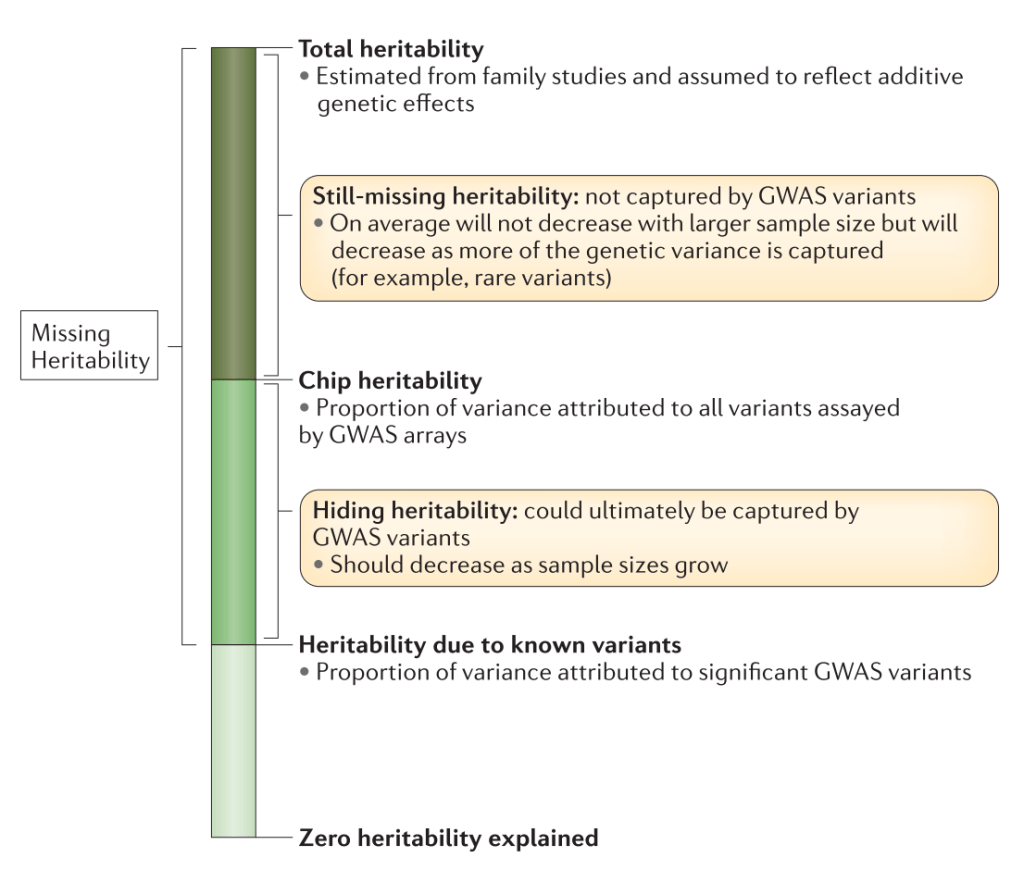图一：三种遗传力的关系。（引自：The contribution of genetic variants to disease depends on the ruler，2014）

Missing and hidden heritability

GWAS研究中一个核心问题便是 Missing heritability，定义为 h2 family 与 h2 GWAS 之间的差值。 h2 GWAS 之所以低于 h2 family ，潜在的原因包括：非加性遗传效应（尽管目前证据很少），效应量大的稀有变异（rare variants），或是双胞胎研究中由于共同的环境因素而造成的过高估计。

Missing heritability 又可细分为 still- missing heritability 与 hidden heritability 。 still- missing heritability 为 h2 family 与 h2 SNP 之间的差，Yang 认为可能的原因是在GWAS研究中由于样本数量的限制，大多数效应量较小的遗传效应无法被可靠地检测。

而 hidden heritability 则为 h2 SNP 与 h2 GWAS 的差。对它的理解建立在Fisher最初对于无穷小模型（infinitesimal model），即多数变异都只有很小的效应。在GWAS研究中，由于我们所选显著阈值的高低，遗传力或许并不是消失（ missing ）而是被隐藏（ hidden ）了。另一种可能则是，人群的异质性（heterogeneity.），因为 h2 GWAS 大多来自包含多群体的meta分析，而遗传效应在这些群体中的异质性也可能使 h2 GWAS 偏低。

如何估计SNP遗传力：

使用GCTA （GREML）来估计SNP-遗传力 SNP Heritability

参考：

An Introduction to Statistical Genetic Data Analysis.

连锁不平衡 linkage disequilibrium LD

连锁不平衡（linkage disequilibrium）是进化生物学与人类遗传学中一个十分重要的概念，因为遗传过程中很多因素能够影响它，而它又会作用于很多因素，包括选择，重组频率，突变率，遗传漂变，交配模式，群体结构等等。反过来看，连锁不平衡就是反应群体遗传过程的一个强有力的信号。

连锁不平衡 是指不同基因座（loci）的等位基因（allele）之间非随机（nonrandom）的关联。

首先考虑简单的两基因座情况，设有A, B两个基因座，每个基因做各有两个等位基因，分别用1,2表示。假设每个单倍体型的频率如下所示：

由上单倍体型的频率，我们也可以简单计算得到各个等位基因的频率：

如果这两个基因座互相独立不相关（也就是连锁平衡 linkage equilibrium 的状态），那么各个单倍型的频率就可以直接算出，为p1q1 ,p1,q2 , p2q1, p2q2

而实际情况中单倍型的频率对于不相关情况下的理论值会产生偏离（deviation），这个偏离原因即为连锁不平衡（ linkage disequilibrium ），偏离的程度通常记为 D （连锁不平衡系数，coefficient of linkage disequilibrium）

$D = x_{11} - p_1q_1$