GWAS 全基因组关联分析 – 第 7 页 – GWASLab

使用GCTA （GREML）来估计SNP-遗传力 SNP Heritability

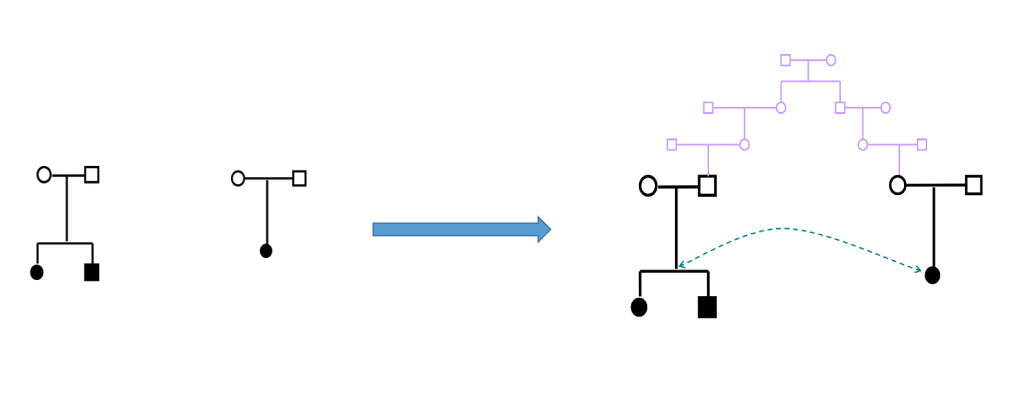
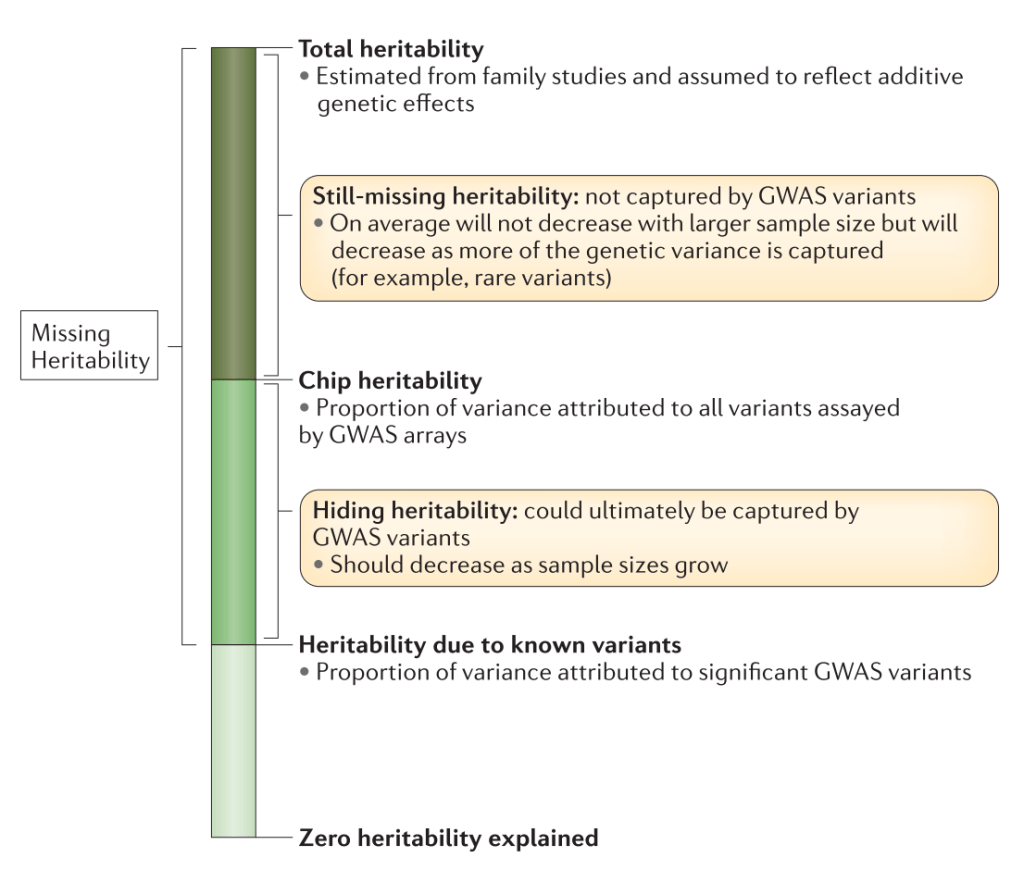
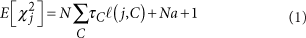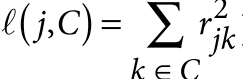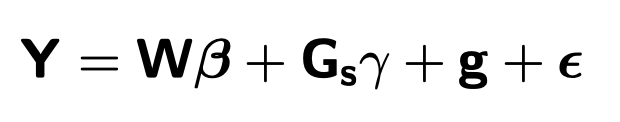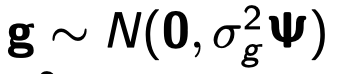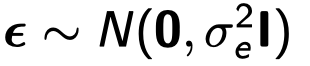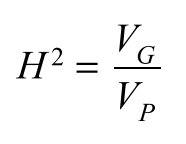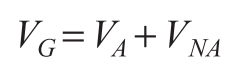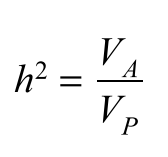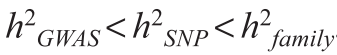GWAS研究中发现的显著SNP只能解释人类群体中复杂性状很小一部分的遗传变异。那么剩余的遗传力在哪里？很多时候这部分遗传力并没有丢失，而是由于部分snp效应太小以至于无法达到显著水平而没有被检测到。

与单SNP关联检验相对，GCTA中的GREML（genome-based restricted maximum likelihood）方法使用线性混合模型（ linear mixed models ， LMMs），将全部SNP的效应作为随机效应拟合。

模型如下：

y是一个n × 1 的表型向量，n是样本大小； β 是固定效应的向量，诸如性别、年龄、以及一个或多个主成分（PC）； u 是SNP效应的向量，服从如下分布：

I 是一个 n × n 的单位矩阵, ɛ 是残余效应的向量，服从以下分布：

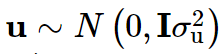
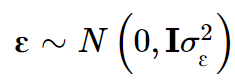
W是标准化的基因型矩阵，其中第ij^th 个元素为：

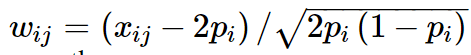
其中 x_ij 是第j个个体的第i个SNP的参考allele的拷贝数， p_i该 allele 的频率。如果我们定义 A = WW^′/N 并且定义 σ2g 为全部SNP解释的方差 , 即 σ2g=Nσ2u, （N为SNP的数量），那么方程 1 等价于：

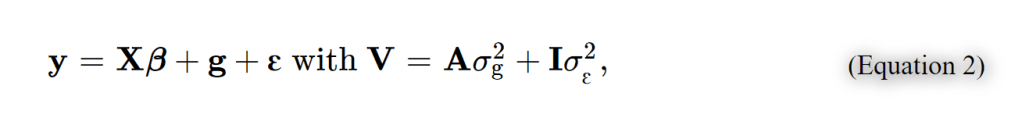
其中g是一个n x 1的向量，表示各个个体的全部的遗传效应，服从 g∼N(0,Aσ2g) 。A 可以理解为个体两两间遗传关系组成的遗传关系矩阵 genetic relationship matrix (GRM) 。于是基于这个线性混合效应模型我们就可以通过估计的GRM，利用REML（ restricted maximum likelihood ）算法来无偏地估计全部SNP解释的方差 σ2g （继而估计SNP遗传力）。

基于以上定义，个体j与个体k的遗传关联可以由以下方程估计：

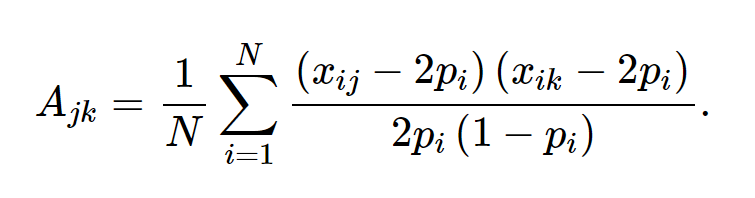
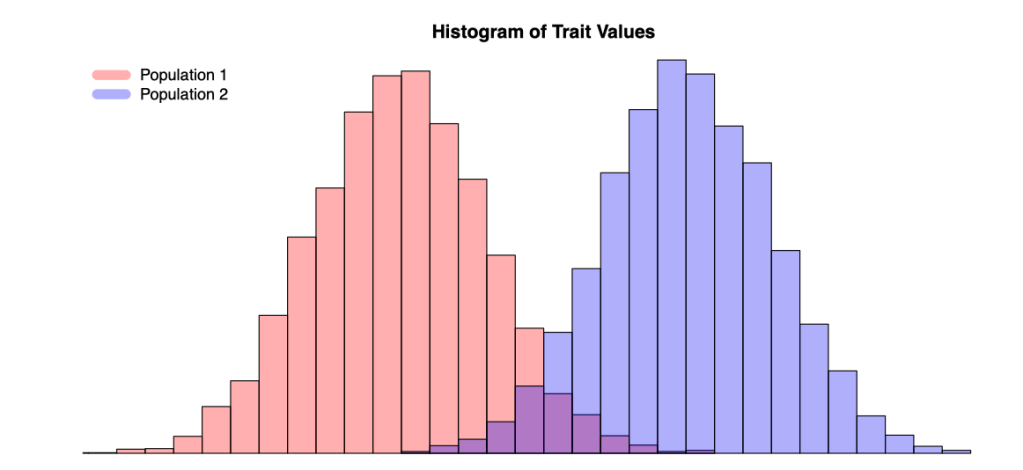
实际操作中我们首先需要排除掉有亲缘关系的个体，主要原因是该模型的目的是估计所有SNP解释的方差，如果纳入有亲缘关系的个体，会由于表型关联（ phenotypic correlations ）而造成偏差，例如由于共同的环境因素。即使没有上述的偏差，那么对它的解读也会有别于 “无关联的”个体：一个基于家系的估计值捕捉的是所有因果变异的贡献，而该方法捕捉的则是与被基因分型的SNP处于LD的因果变异的贡献。

下面简单介绍如何利用GCTA软件估计snp-遗传力：

GCTA下载链接：https://cnsgenomics.com/software/gcta/#Download

GCTA语法上类似PLINK，文件格式也几乎通用，使用起来十分便捷：

第一步：估计GRM

gcta64 --bfile test --autosome --maf 0.01 --make-grm --out test --thread-num 10

输入为plink格式的bed/bim/fam文件，

–autosome 只是用常染色体上的SNP
–maf 0.01 过滤掉maf小于0.01的snp
–make-grm 计算GRM
–out 输出文件的前缀
–thread-num 10 要使用的线程数

计算完成后GRM会存储在以下文件中： test.grm.bin, test.grm.N.bin and test.grm.id

我们也可以去除掉有亲缘关系的个体：

gcta64 --grm test --grm-cutoff 0.025 --make-grm --out test_rm025

第二步：利用GCTA-GREML估计SNP遗传力

gcta64 --grm test --pheno test.phen --reml --out test --thread-num 10

–pheno 表型文件
–reml 利用reml算法计算snp遗传力

计算结果储存在 test.hsq的文件中

当然我们以可以加入协变量，例如前10个主成分 PC1-10：

gcta64 --grm test --pheno test.phen --reml --qcovar test_10PCs.txt --out test --thread-num 10

对于较大的数据量，我们还可以分染色体进行计算，详见：https://cnsgenomics.com/software/gcta/#Tutorial

参考：

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3014363/

Yang, J. et al. Common SNPs explain a large proportion of the heritability for human height. Nature Genetics 42, 565–569 (2010).

https://cnsgenomics.com/software/gcta/#Overview

https://cnsgenomics.com/software/gcta/#Tutorial

基于功能分类分割遗传力 – 分层LD分数回归 Stratified LD score regression

在复杂性状的GWAS研究中，大部分遗传力由并没有达到全基因组显著性水平的SNP关联贡献。然而当前许多利用功能信息与GWAS数据来研究疾病的方法仅仅使用达到显著性水品的loci里的SNP，并且只假设每个loci里只有一个因果SNP，或是完全不考虑LD。基于这些不足，本方法的作者们期望使用所有SNP的信息，并明确的将LD纳入模型，来估计每个功能分类的SNP遗传力，以提升power。

本方法是在基础的LD分数回归上的延伸，可以参考：

连锁不平衡分数回归 LD score regression
遗传相关跨性状的LD分数回归（预留链接）

在此之前分割SNP遗传力的方法借助REML（ restricted maximum likelihood ），例如GCTA，但需要个体的基因型的原始数据，并且需要很大的计算资源。所以作者们开发了分层LD分数回归，只需要GWAS的 summary statistics ，以及从与目标群体相对应的参考群体中计算得到的LD信息。

该方法的核心基于以下的一个事实， GWAS中某个SNP的χ² 检验统计量包含了所有被该SNP标记的SNP的效应。因此对于一个多基因性状，一个有高LD分数的SNP，相比于低 LD分数的SNP ，总体上也会有较高的 χ² 检验统计量。原因主要是这些SNP可能标记了单个有很大效应量的SNP，或是多个较弱效果的SNP。（也就是 “以一敌百” 或者 “人多力量大”）

所以我们将所有SNP分为具有不同遗传力的功能分类，那么与某个高遗传力分类存在LD的SNP就会有更高的 χ² 检验统计量 。如果与某个功能分类存在高LD的SNP有较高的 χ² 检验统计量，那么就定义这个功能分类有遗传力聚集。

在多基因模型下，某个SNP j 的 χ² 检验统计量 的期望值为

N为样本大小
C则是功能分类的索引
l(j,C)则是SNP j 对于分类C的LD分数

a则衡量了混淆因素的大小
τC则表示了每个SNP对于功能分类C遗传力的贡献。

该方程使我们可以估计 τC 的大小（也就是所谓的分割的遗传力）。定义某个分类的聚集为该分类SNP遗传力的比例除以该分类SNP总数的比例。

该方法的作者们基于多个公开的注释数据库，构建了不针对任何细胞类型的全基线模型 ‘full baseline model’ ，包括 coding, UTR, promoter and intronic regions the histone marks monomethylation (H3K4me1) and trimethylation (H3K4me3) of histone H3 at lysine 等等。除此之外，还基于全基线模型，构建了多个针对特定细胞类型的模型，包含针对细胞类型的注释等。

尽管Stratified LD score regression提供了一种便捷有效的分析 GWAS的 summary statistics 的方法，但我们也要同时注意该方法的不足之处：

为了达到足够的power，需要较大的样本量，或是较大的SNP遗传力，而且性状必须是多基因的
该方法需要针对研究群体的LD参考数据
该方法目前不支持自定义的array
该方法基于加性模型，没考虑上位或非加性的效应
该方法依赖于可用的功能注释，如果没有相应注释则无法检测
等等

使用方法：

下载，安装，配置环境，数据清理详见

连锁不平衡分数回归 LD score regression

除了以上步骤外，我们还需要下载相应的baseline模型：

https://alkesgroup.broadinstitute.org/LDSCORE/

从以上链接中我们需要下载以下内容（以欧洲群体为例）：

基线模型LD分数：baseline.* in 1000G_Phase1_baseline_ldscores.tgz
频率：1000G.mac5eur.* in 1000G_Phase1_frq.tgz
权重：weights.* in weights_hm3_no_hla.tgz

解压后即可使用：

python ldsc.py 
	--h2 BMI.sumstats.gz\
	--ref-ld-chr baseline.\ 
	--w-ld-chr weights.\
	--overlap-annot\
	--frqfile-chr 1000G.mac5eur.\
	--out BMI_baseline

–h2 ：计算分割的遗传力，参数为之前处理好的gwas summary statistics
--ref-ld-chr ：下载的参考LD分数文件
--w-ld-chr：权重文件
--frqfile-chr： SNP频率文件
--overlap-annot：表示基线模型中功能分类有重叠
–out：指定出输出文件的前缀

参考：

http://www.github.com/bulik/ldsc

https://github.com/bulik/ldsc/wiki/Partitioned-Heritability

Partitioning heritability by functional annotation using genome-wide association summary statistics https://www.nature.com/articles/ng.3404

GWAS的线性混合模型LMM Linear Mixed Model

关键词：population structure，cryptic relatedness，spurious association，LMM，GRM

早期的GWAS研究使用的模型为固定效应的线性模型，但通常会受两方面混淆因素的影响：

群体结构/分层（population structure/ stratification）：研究群体中存在有不同祖先（ancestry）的亚群体（subgroup）
隐性关联（cryptic relatedness）：研究样本之间存在未知的亲缘关系

如果在模型中故意忽略掉这些混淆变量（confounding variable），就很可能导致结果出现假阳性（false positive）或是虚假关联（spurious association），所以这是我们在进行GWAS研究时，必须要考虑的问题。

Population structure

首先来看群体结构/分层

考虑一个case-control研究，如下图所示，红色的群体在整体样本中占了case的大多数，那么一些对疾病并没有影响，但在红蓝两群体之间等位基因频率相差很大的genetic marker，就有可能会造成虚假关联（spurious association）。

为了解决这个问题，我们通常会采用genomic control的方法，或是通过PCA来矫正。详见：

Genomic control (基因组控制与基因组膨胀系数λ Genomic control λGC)
PCA （群体分层与主成分分析 Population structure & PCA）

Cryptic relatedness

由于将主成分作为协变量纳入模型以矫正群体分层的方法，适用于样本中不存在亲缘关系的情况下使用，而样本中存在亲缘关系时，就不一定有效，但通常我们的研究中都会存在有亲缘关系的样本。

当样本中存在隐性关联 / 错误认定的关联 Cryptic and / or misspeciﬁed relatedness时，也可能会造成上述的虚假关联。由于我们通常不能掌握所有研究对象的家谱，所以无法完全去相关个体，例如下面的情况，样本中看似不相关的个体间实际上存在隐性关联：

Linear Mixed Model

为了解决以上问题，相比早期的线性模型，我们就采用一种更为灵活的模型，线性混合模型来进行检验。

固定效应 fixed effects：

W为 n x （w + 1）的矩阵，包含了截距，以及协变量
β 则是 ( w + 1 ) × 1 的向量，表示协变量的效应量
Gs为 n × 1 的向量，某个位点的基因型，每一项的值通常为 0，1，2（等位基因allele的拷贝数）
γ则是标量，目标位点基因型的效应量

随机效应 random effects：

g为长度为n的随机向量，表示多基因效应

δ2g为加性遗传方差
Ψ是成对遗传相关的矩阵
e是长度为n的随机向量，服从以下的分布，其中δ2e为非遗传效应造成的方差，我们认为这项在个体间是相互独立的

这样我们就构建了包含群体结构和隐形相关的模型。

通常成对遗传相关的矩阵Ψ是未知的，在计算中我们使用empirical GRM（genetic relatedness matrix，通过纳入研究的SNP计算得出）

目前已有多种GWAS检验方法基于LMM模型，包括：

EMMAX
GEMMA
GMMAT
Bolt-LMM
fastGWAS
SAIGE
等等

参考：

Lecture 6: GWAS in Samples with Structure ，Summer Institute in Statistical Genetics 2015

GWAS线性混合模型中的LOCO Leave-one-chromosome-out

关键词：LMM，proximal contaminal, LOCO

目前的GWAS已经开始逐渐使用线性混合模型（ linear mixed models ，LMM）来代替早期的线性模型，主要原因是线性混合模型能够校正多种原因造成的混淆，例如遗传关联（ genetic relatedness ），家庭关联（ familial relatedness ），群体分层（ population structure ）等，LMM模型也因此能够控制假阳性，并提高检验power。

但在使用混合线性模型中一个重要的问题就是，当我们在GRM中纳入了被检验的SNP时，反而会导致power降低。原因是在模型中我们对待检测SNP进行了二重拟合（ double-fitting ），即:

1 . 作为检验关联时的固定效应（fixed effect）
2. 在GRM中作为随机效应（random effect）

这种现象就被称为 临近污染 “proximal contamination”。

为了避免此现象造成的power损失，理论上在构建null模型中排除掉待检验SNP是正确的做法，但这样太占运算资源，所以在实践中，我们会采用 LOCO Leave-one-chromosome-out ，即使用排除掉待检验SNP所在的染色体的所有SNP，再进行检验（也就是说我们有对应22个常染色体的loco null模型）。

目前主流的软件都已支持loco，只需要–loco 指定即可。

参考：

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3597090/

Advantages and pitfalls in the application of mixed-model association methods

GWAS的条件分析 Conditional analysis

关键字：conditional analysis，leading SNP, secondary casual variants , fine-mapping

GWAS研究中，对于某个复杂表型，我们会发现很多显著关联的基因座（loci），每个基因座里有若干显著的SNP，这些SNP通常处于LD。这时我们就会面临一个问题，这个基因座里显著的SNP单单因为与leading SNP（该loci里P值最低的SNP）连锁不平衡而显著，还是因为这个SNP本身就与就与表型相关联。这时就应该进行条件分析（conditional analysis），实际上是一种fine-mapping（对casual SNP 致病SNP的精确定位）的方法，目的是确认是否存在次要的因果SNP secondary causal variants。

一般来说进行条件分析的方法很简单，

1.从GWAS结果中抽出每个关联基因座的leading SNP，

2.将该leading SNP作为协变量加入检验模型

3.再次进行关联检验，确认关联基因座里除 leading SNP 以外还是否有次要的致病SNP secondary causal variants。

例如下图所示的情况：

图1：针对橙色圈中的leading SNP （该loci里p值最低），进行条件分析后的曼哈顿图。A：该loci只有一个信号，表示没有 secondary causal variants ，之所以有多个显著snp是因为与leading SNP处于连锁不平衡。B：除了leading SNP 还有其他信号，表示这个loci还存在 secondary causal variants 。

通常conditional analysis的功能已经集成在关联检验的软件中（如PLINK，SAIGE），我们只需要提供lead snp的 id 或是位置，就可以进行条件分析了。

例如：

PLINK中的 –condition 选项，也可以使用 –condition–list(同时将多个SNP作为covariate纳入检验模型)

SAIGE 第二步中，也提供了 –condition 选项，可以对单个或多个snp进行条件分析

参考：

Strategies for fine-mapping complex traits.

https://www.cog-genomics.org/plink/1.9/assoc

https://github.com/weizhouUMICH/SAIGE/wiki/Genetic-association-tests-using-SAIGE

遗传力 Heritability 与 Missing heritability

本文关键词： Heritability， h2, family heritability , SNP heritability, GWAS heritability , Missing heritability

遗传力的基础概念

遗传力（Heritability）是我们理解遗传与环境因素对性状影响的基础，定义为遗传方差占性状方差（总方差）的比值，可以理解为遗传因素对性状的影响，数学上以h2表示。

通常根据对遗传方差的定义而分为广义与狭义遗传力：

广义遗传力 broad-sense heritability ：

其中VP = VG + VE, VP为性状方差，VE为环境方差（也包括测量误差等），而分子的VG为遗传方差。

遗传方差VG也可进一步细分为

VA是加性遗传效应的方差，VNA是非加性遗传效应的方差（上位与显性遗传效应）

加性遗传效应是指当两个或多个基因对于某一性状，或是单个基因的不同等位基因对于某一性状的整体作用，等于它们单独作用之和。

非加性遗传效应则包括上位与显性遗传效应。

因为对于绝大多数复杂性状，很少有证据证明有非加性遗传效应存在，所以我们目前聚焦于主要考虑加性遗传效应的狭义遗传力，

狭义遗传力 narrow-sense heritability ：

遗传力的估计

我们有多种方法可以估计遗传力h2的大小，目前主要的方法有三种，通过双胞胎研究，SNP或是GWAS来估计。

h2 family ：双胞胎研究，通过比较同卵与异卵双胞胎的相似性，计算得到h2，通常为这三种中最高。

h2 SNP ：GWAS研究所用chip上所有variants共同解释的方差与性状方差的比值，比 h2 family 低，但会显著高于h2 GWAS。可以使用GCTA的GREML模型来估计。（使用GCTA （GREML）来估计SNP-遗传力 SNP Heritability ）

h2 GWAS ：仅由GWAS所发现的某疾病相关variants解释的方差与性状方差的比值，三者中最低。

一般情况下，三者的关系：

更直观的关系如下图所示：

图一：三种遗传力的关系。（引自：The contribution of genetic variants to disease depends on the ruler，2014）

Missing and hidden heritability

GWAS研究中一个核心问题便是 Missing heritability，定义为 h2 family 与 h2 GWAS 之间的差值。 h2 GWAS 之所以低于 h2 family ，潜在的原因包括：非加性遗传效应（尽管目前证据很少），效应量大的稀有变异（rare variants），或是双胞胎研究中由于共同的环境因素而造成的过高估计。

Missing heritability 又可细分为 still- missing heritability 与 hidden heritability 。 still- missing heritability 为 h2 family 与 h2 SNP 之间的差，Yang 认为可能的原因是在GWAS研究中由于样本数量的限制，大多数效应量较小的遗传效应无法被可靠地检测。

而 hidden heritability 则为 h2 SNP 与 h2 GWAS 的差。对它的理解建立在Fisher最初对于无穷小模型（infinitesimal model），即多数变异都只有很小的效应。在GWAS研究中，由于我们所选显著阈值的高低，遗传力或许并不是消失（ missing ）而是被隐藏（ hidden ）了。另一种可能则是，人群的异质性（heterogeneity.），因为 h2 GWAS 大多来自包含多群体的meta分析，而遗传效应在这些群体中的异质性也可能使 h2 GWAS 偏低。

如何估计SNP遗传力：

使用GCTA （GREML）来估计SNP-遗传力 SNP Heritability

参考：

An Introduction to Statistical Genetic Data Analysis.

连锁不平衡 linkage disequilibrium LD

连锁不平衡（linkage disequilibrium）是进化生物学与人类遗传学中一个十分重要的概念，因为遗传过程中很多因素能够影响它，而它又会作用于很多因素，包括选择，重组频率，突变率，遗传漂变，交配模式，群体结构等等。反过来看，连锁不平衡就是反应群体遗传过程的一个强有力的信号。

连锁不平衡 是指不同基因座（loci）的等位基因（allele）之间非随机（nonrandom）的关联。

首先考虑简单的两基因座情况，设有A, B两个基因座，每个基因做各有两个等位基因，分别用1,2表示。假设每个单倍体型的频率如下所示：

由上单倍体型的频率，我们也可以简单计算得到各个等位基因的频率：

如果这两个基因座互相独立不相关（也就是连锁平衡 linkage equilibrium 的状态），那么各个单倍型的频率就可以直接算出，为p1q1 ,p1,q2 , p2q1, p2q2

而实际情况中单倍型的频率对于不相关情况下的理论值会产生偏离（deviation），这个偏离原因即为连锁不平衡（ linkage disequilibrium ），偏离的程度通常记为 D （连锁不平衡系数，coefficient of linkage disequilibrium）

$D = x_{11} - p_1q_1$

下图表示了各单倍型频率，各等位基因频率与D之间的关系。

但要注意的是，D值并不是一个用来衡量LD的很好的指标，因为D值会受等位基因频率影响，这使得我们无法比较不同频率的等位基因对之间连锁不平衡的大小。

Lewontin提出通过标准化D值来解决该问题，即用D值除以理论上D可能的最大绝对值：

$D' = {{D}\over{D_{max}}}$

其中D的理论最大绝对值为：

$D_{max} = \begin{cases} max\{-p_1p_2, -(1-p_1)(1-p_2)\}, \text{when } D < 0 ,\\ min\{p_1(1-p_2), (1-p_1)(p_2)\}, \text{when } D > 0. \end{cases}$

但更多的时候我们使用相关系数（correlation coefficient）r2来衡量LD：

$r^2 = {{D^2}\over{p_1(1-p_1)p_2(1-p_2)}}$

Locuszoom等绘制regional plot的软件会用到r2。

一些Fine-mapping分析软件中则会使用到r，其主要区别是 r 会分单倍体型。

参考：

https://en.wikipedia.org/wiki/Linkage_disequilibrium

Montgomery Slatkin. Linkage disequilibrium — understanding the evolutionary past and mapping the medical future.

勘误：

2024/02/19 修改了Dmax式子中D>0 与 D<0写反的错误。感谢 @Rain 的指正。

哈迪温伯格平衡 Hardy– Weinberg equilibrium

哈迪温伯格平衡是群体遗传学中一个十分重要的概念，它描述了在一个群体中某基因型的概率与分布。

具体来讲，哈迪温伯格平衡是指等位基因与基因型的频率，在无其他进化干扰因素存在的情况下，在代与代之间将会保持恒定。

换一句话说，如果某个群体里对于某个基因来说处于哈迪温伯格平衡，那么就可以说这个基因没有在进化，该基因的等位基因频率在代与代之间也会保持恒定。

但哈迪温伯格平衡需要满足以下假设：

没有自然选择 no natural selection
没有遗传漂变 no genetic drift
一个封闭的群体，没有大规模迁入迁出 no significant migration in or out of the population
没有变异 no mutations
没有选型交配 no assortative mating
没有近亲交配 no inbreeding

在某一满足哈迪温伯格平衡假设的群体中，设 p为等位基因A的频率，q为等位基因a的频率；那么p2, 2pq, q2就表示个基因型的概率；

哈迪温伯格平衡可以用如下的公式表示：

如果p=0.3 ， q=0.7，那么AA的频率就为9%，Aa为42%，aa为49%。

参考资料：

An Introduction to Statistical Genetic Data Analysis

SNP数据库 – dbSNP

链接： https://www.ncbi.nlm.nih.gov/snp/

1.dbSNP简介

dbsnp是NCBI于1998年建立的主要存储单核苷酸多态性（SNP）的免费公共数据库。该数据库包含多种模式生物。虽然其名称为dbSNP，但该数据库实际上包括多种分子变异：

单核苷酸多态性 SNP
短缺失和插入多态性 short deletion and insertion polymorphisms (indels/DIPs)
微卫星标记或短串联重复 microsatellite markers or short tandem repeats (STRs)
多核苷酸多态性 multinucleotide polymorphisms (MNPs)
杂合序列 heterozygous sequences
命名变体 named variants

2. 网页版dbsnp中的SNP信息 (本文使用新本界面，也可以切换回旧版)：

首先是snp的基础信息，包括物种，位置，等位基因，变异类型，频率等等，

此处以rs671为例：

通过切换不同tab可以看到与该snp相关的其他详细信息

最后还可以在基因组浏览器的序列坐标中直观的看到该snp与相邻的其他snp等。

3. 通过FTP下载完整数据：

如果需要下载最新版本的dbsnp数据库则，进入latest_release中，下载bgzip压缩过的VCF文件以及相应的tabix索引

如果需要某个历史版本，则进入archive中，下载对应版本的数据。

参考文献：

GWAS Catalog 数据库

GWAS catalog数据库于2008年由National Human Genome Research Institute (NHGRI)建立，旨在应对快速增长的全基因组关联分析（GWAS）数据。该数据库为我们检索已发表GWAS与显著相关提供了方便。

该数据库中主要包含了已发表GWAS的Summary statistics （人工审核录入，有一定延迟，大约发表后一到两个月内录入数据库）。截止2021年3月25日，GWAS catalog已经收录了4,961篇文献，包括251,401个相关。目前该数据库采用的参考基因组与SNP数据库为Genome Assembly GRCh38.p13 与 dbSNP Build 153。

已发表或未发表的GWAS Summary statistics都可通过GWAS catalog的FTP进行下载。

图2：已发表并有summary statistics的GWAS列表（部分）

Haplotype	Frequency
$A_{1}B_{1}$	$x_{11}$
$A_{1}B_{2}$	$x_{12}$
$A_{2}B_{1}$	$x_{21}$
$A_{2}B_{2}$	$x_{22}$

Allele	Frequency
$A_1$	$p1 = x_{11} + x_{12}$
$A_2$	$p2 = x_{21} + x_{22}$
$B_1$	$q1 = x_{11} + x_{21}$
$B_2$	$q2 = x_{12} + x_{22}$

	$A_1$	$A_2$	Total
$B_1$	$x_{11} = p_1q_1+D$	$x_{21} = p_1q_1-D$	$q_1$
$B_2$	$x_{12} = p_1q_2-D$	$x_{22} = p_2q_2+D$	$q_2$
Total	$p_1$	$p_2$	1