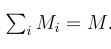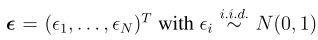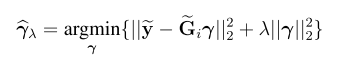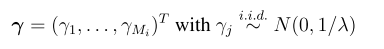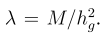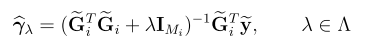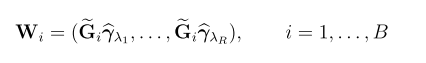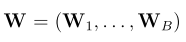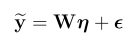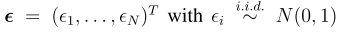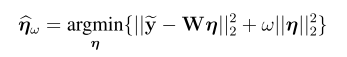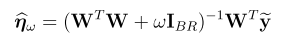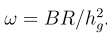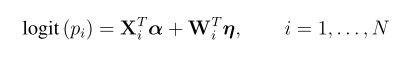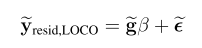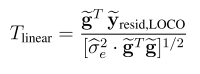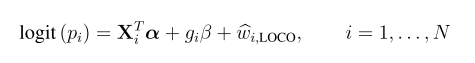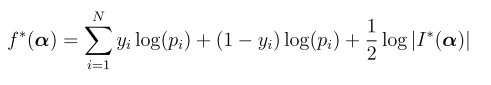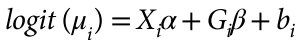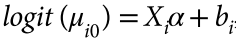05 SNV association analysis – 第 2 页 – GWASLab

GWAS的条件分析 Conditional analysis

关键字：conditional analysis，leading SNP, secondary casual variants , fine-mapping

GWAS研究中，对于某个复杂表型，我们会发现很多显著关联的基因座（loci），每个基因座里有若干显著的SNP，这些SNP通常处于LD。这时我们就会面临一个问题，这个基因座里显著的SNP单单因为与leading SNP（该loci里P值最低的SNP）连锁不平衡而显著，还是因为这个SNP本身就与就与表型相关联。这时就应该进行条件分析（conditional analysis），实际上是一种fine-mapping（对casual SNP 致病SNP的精确定位）的方法，目的是确认是否存在次要的因果SNP secondary causal variants。

一般来说进行条件分析的方法很简单，

1.从GWAS结果中抽出每个关联基因座的leading SNP，

2.将该leading SNP作为协变量加入检验模型

3.再次进行关联检验，确认关联基因座里除 leading SNP 以外还是否有次要的致病SNP secondary causal variants。

例如下图所示的情况：

图1：针对橙色圈中的leading SNP （该loci里p值最低），进行条件分析后的曼哈顿图。A：该loci只有一个信号，表示没有 secondary causal variants ，之所以有多个显著snp是因为与leading SNP处于连锁不平衡。B：除了leading SNP 还有其他信号，表示这个loci还存在 secondary causal variants 。

通常conditional analysis的功能已经集成在关联检验的软件中（如PLINK，SAIGE），我们只需要提供lead snp的 id 或是位置，就可以进行条件分析了。

例如：

PLINK中的 –condition 选项，也可以使用 –condition–list(同时将多个SNP作为covariate纳入检验模型)

SAIGE 第二步中，也提供了 –condition 选项，可以对单个或多个snp进行条件分析

参考：

Strategies for fine-mapping complex traits.

https://www.cog-genomics.org/plink/1.9/assoc

https://github.com/weizhouUMICH/SAIGE/wiki/Genetic-association-tests-using-SAIGE

Regenie – 高效的全基因组回归

本方法由Regeneron Genetics Center开发，regenie基于一种机器学习方法（Stacked block ridge regression）。Regenie相比于之前的基于LMM的方法，如bolt-LMM，fastGWA，以及SAIGE等方法，具有以下主要特点：

1 相比其他方法更快，更省内存。
2 可适用于数量表型，或是二分类表性。
3 可以同时对多个表型进行检验。
4 可以矫正在case-control不平衡时，mac过低造成的SNP效应值的过高估计（SAIGE-SPA存在此问题）。

regenie 方法简介：

regenie与saige或fastGWA一样，同样采用了两个步骤的模式来进行检验。

STEP 1，估计空模型（主要利用 Stacked block ridge regression的方法）

1 层叠区块脊回归 Stacked block ridge regression

1.1 分割区块 Block partitions

将转化后的基因型矩阵G分割为B个连续的区块，每个区块所包含的SNP都来自同一条染色体。定义区块的方法有很多种，例如物理距离，遗传距离等等，实际使用中，一般将区块大小固定。设mi为第i个区块的SNP数量，则有：

1.2 0级脊回归 Level 0 ridge regressions

这一步的目的是减小估计值的数量，使估计值能够捕获（1）区块中SNP之间的LD信息（2）SNP对表性的任何效应。

这一步考虑拟合带有L2惩罚项的线性模型（也就是脊回归）。

其中，

我们可以通过以下式子估计SNP的效应值γ

其中λ为收缩系数， λ 越高会使估计的效应值趋近于0. 效应值得估计也可以被视为贝叶斯框架下的最大后验估计值（MAP），这个框架里对于SNP效应值，我们使用一个正态先验概率：

基于以上假设，我们可以将脊回归的收缩系数视为一个SNP遗传力的方程，即

由于我们并不知道SNP对于表型真实的效应值，所以考虑使用一组系数来反应SNP的遗传力可能的值。

更准确的说，就是选择R个介于0到1之间等间隔的值。然后利用该值来计算λ。

对于每个大小为Mi的区块，我们都可以计算出R个估计值，

第一步的结果就是一个Nx（BR）的预测值矩阵。

1.3 1级脊回归 Level 1 ridge regression

为了进一步整合第一步结果W中的预测值，在第一步脊回归的基础上再次脊回归（称为stacking），目的是通过惩罚项获得一个最优化的区块预测值的线性组合。

通过变换使W有单位方差，然后进行第二次脊回归，有

其中

该式的解可以由以下式子表示，

该式有一个封闭的解

同第一次脊回归一样，超系数w从一组个数为Q的收缩系数中选择。

一个最适的w*通过最小化预测值误差来获得，

1.4 K-fold cross-validation

由于W与表型相关，采用K-fold cross-validation来避免过拟合。

1.5 LOCO

为了避免近端污染（proximal contamination），在 cross-validation 的计算中会将一整条染色体的区块的值，设为0。这样最终，我们会有22个预测值。

1.6 对于二分类表型，

第一次回归与数量表型一样，但在第二次回归时，采用逻辑斯蒂回归而不是脊回归。

STEP 2 关联检验 Association testing

第二步，检验，

2.1 对于数量表型，考虑一下模型，

使用分数检验，统计量如下：

2.2 对于二分类表型，采用以下模型

2.3 Firth logistic regression（重点）

当case-control不平衡时，稀有变异的检验通常会有不稳定的效应估计值与标准差，主要是在逻辑斯蒂回归中，case里不存在minor allele时会出现拟完全分离（quasi-complete separation）。解决方案之一便是，在逻辑斯蒂回归中加入一个惩罚项，

但这个方法计算量巨大，所以regenie使用了近似的 Firth logistic regression ，使用了一个调整后的惩罚项：

这样就大大减少了计算量，最后应用likelihood ratio test (LRT) 来检验。

2.4 regnie在第二步中也支持saige所使用的SPA方法。这里就略过。

最后放上文章中的总结图：

参考：

https://rgcgithub.github.io/regenie/

https://www.biorxiv.org/content/10.1101/2020.06.19.162354v2

SAIGE

关键词：saige，GLMM，case-control imbalance

一句话解释：SAIGE是一种针对二分类表型（binary phenotype）能够调整样本对照不平衡（case-control imbalance）与隐性关联（cryptic relatedness）的检验方法。

saige 与 bolt-lmm 或 regenie 类似，都需要两个步骤。saige使用的是GLMM模型：

具体流程如下：

第一步（构建null模型）：利用 array genotype ，估计 null 逻辑斯蒂混合模型（GLMM）。

通过PQL方法和 AI-REML 算法简化计算提高效率。

隐性关联由随机效应解释。

第二步（检验）：分数检验，并通过SPA调整。

saige方法之所以能调节 case-control不平衡，关键点就在于利用SPA对检验的调整。

SPA：

（未完待续）