分类： GWAS 全基因组关联分析

多基因风险分数 PRS( Polygenic risk score)系列之九: 使用PLINK2分染色体计算PRS并加和

本文内容：

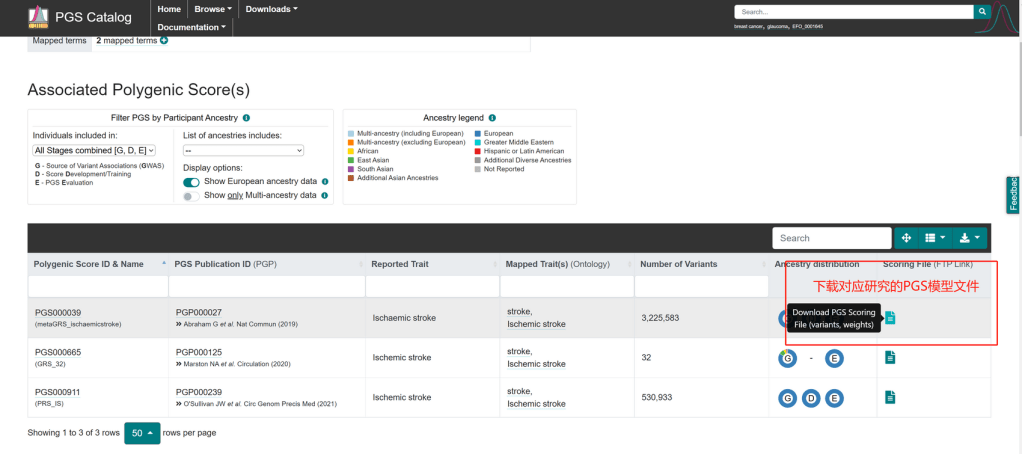
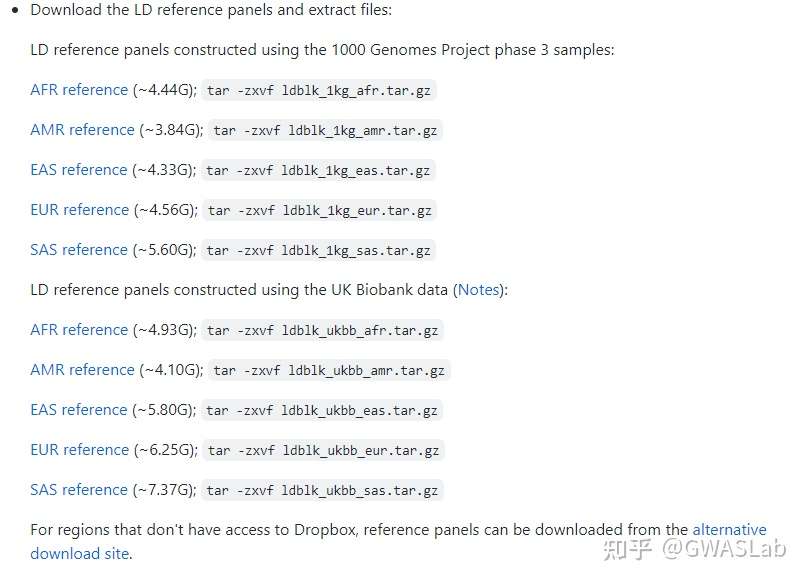
  1. 下载PGS分数文件
  2. 第一步 计算每条染色体的原始分数
  3. 第二步 将各个染色体的结果提取
  4. 第三步 将分数进行简单加和

本文主要演示分染色体计算PRS并求和的过程。

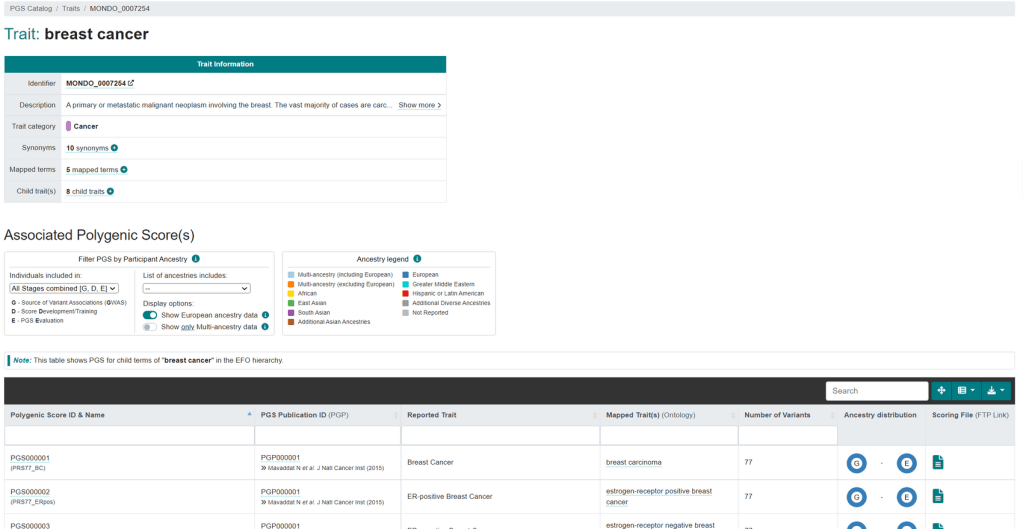
下载PGS分数文件 Download PGS score

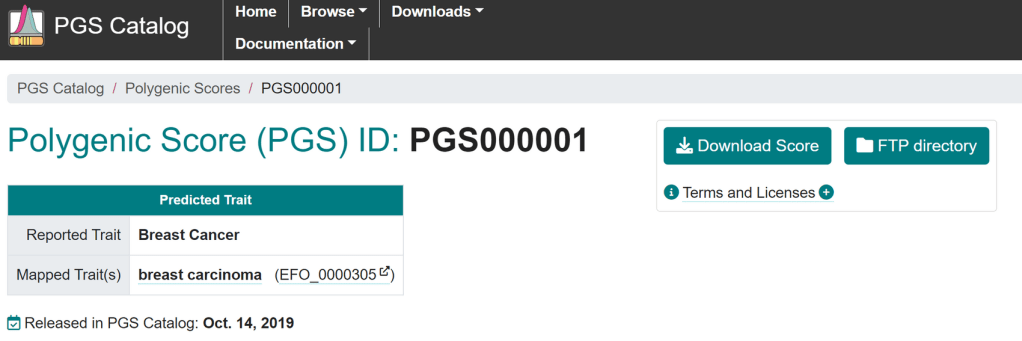
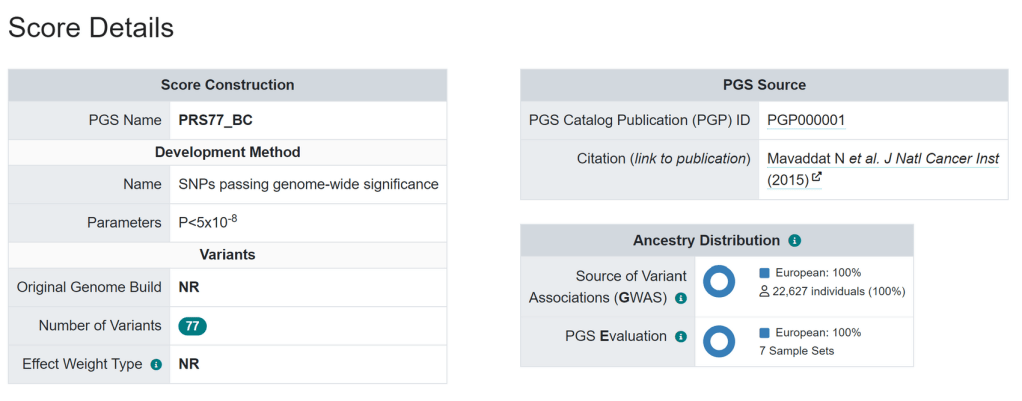
演示PGS分数文件下载自PGScatalog

下载harmonise后的文件：

wget https://ftp.ebi.ac.uk/pub/databases/spot/pgs/scores/PGS000012/ScoringFiles/Harmonized/PGS000012_hmPOS_GRCh37.txt.gz
gunzip PGS000012_hmPOS_GRCh37.txt.gz
head PGS000012_hmPOS_GRCh37.txt
###PGS CATALOG SCORING FILE - see <https://www.pgscatalog.org/downloads/#dl_ftp_scoring> for additional information
#format_version=2.0
##POLYGENIC SCORE (PGS) INFORMATION
#pgs_id=PGS000012
#pgs_name=GRS49K
#trait_reported=Coronary artery disease
#trait_mapped=coronary artery disease
#trait_efo=EFO_0001645
#genome_build=hg19
#variants_number=49310

#下载后去除文件头部的comment，方便Plink2使用
awk '$1!~/#/{print $0}' PGS000012_hmPOS_GRCh37.txt > PGS000012_hmPOS_GRCh37_plink2.txt

head PGS000012_hmPOS_GRCh37_plink2.txt
rsID    effect_allele   effect_weight   hm_source       hm_rsID hm_chr  hm_pos  hm_inferOtherAllele
rs1333045       C       0.187251        ENSEMBL rs1333045       9       22119195        T
rs1537370       T       0.17296 ENSEMBL rs1537370       9       22084310        C
rs9863247       T       0.136328        ENSEMBL rs9863247       3       161125373       C
rs11203077      T       0.131725        ENSEMBL rs11203077      10      91097085        G
rs10268558      C       0.12966 ENSEMBL rs10268558      7       18924927        T
rs7148203       C       0.128366        ENSEMBL rs7148203       14      45062275        T
rs12747328      T       0.127016        ENSEMBL rs12747328      1       159429702       C
rs17810947      G       0.126626        ENSEMBL rs17810947      18      70754886        A/T
rs2412710       A       0.125677        ENSEMBL rs2412710       15      42683787        G

基因组文件使用 https://choishingwan.github.io/PRS-Tutorial/plink/ 所提供的的EUR文件

EUR.QC.bed
EUR.QC.bim
EUR.QC.fam

注：本教程计算结果无实际意义，仅为演示计算过程使用。

第一步 计算每条染色体的原始分数 step1 calculate the raw scores for each chromosome

score=PGS000012_hmPOS_GRCh37_plink2.txt

for chr in $(seq 1 22)
do
plink2 \
    --bfile ./EUR.QC \
    --score ${score} 1 2 3 header list-variants cols=+scoresums \
    --chr ${chr} \
    --out EUR_CAD.chr${chr} 
done

—score 后跟 分数文件路径， 并指定 文件的 ID, effect allele 以及 effect_weight的列数。

header ：分数文件有header，计算时会自动跳过第一行

list-variants ： 将计算所用的所有variant ID写进plink2.sscore.vars

—chr 指定所计算的染色体编号

注1： 这里要加上cols=+scoresums 来获取原始结果，默认输出的仅为平均后的结果

--score applies one or more linear scoring systems to each sample, and reports results to plink2.sscore. More precisely, if G is the full genotype/dosage matrix (rows = alleles, columns = samples) and a is a scoring-system vector with one coefficient per allele, --score computes the vector-matrix product aTG, and then divides by the number of variants when reporting score-averages.

注2：有时候分数文件中不包括某些染色体的variants，所以有些染色会计算失败，求和时应注意

所得文件

EUR_CAD.chr10.log          EUR_CAD.chr15.log          EUR_CAD.chr1.log           EUR_CAD.chr3.log          EUR_CAD.chr8.log
EUR_CAD.chr10.sscore       EUR_CAD.chr15.sscore       EUR_CAD.chr1.sscore        EUR_CAD.chr3.sscore       EUR_CAD.chr8.sscore
EUR_CAD.chr10.sscore.vars  EUR_CAD.chr15.sscore.vars  EUR_CAD.chr1.sscore.vars   EUR_CAD.chr3.sscore.vars  EUR_CAD.chr8.sscore.vars
EUR_CAD.chr11.log          EUR_CAD.chr16.log          EUR_CAD.chr20.log          EUR_CAD.chr4.log          EUR_CAD.chr9.log
EUR_CAD.chr11.sscore       EUR_CAD.chr16.sscore       EUR_CAD.chr20.sscore       EUR_CAD.chr4.sscore       EUR_CAD.chr9.sscore
EUR_CAD.chr11.sscore.vars  EUR_CAD.chr16.sscore.vars  EUR_CAD.chr20.sscore.vars  EUR_CAD.chr4.sscore.vars  EUR_CAD.chr9.sscore.vars
EUR_CAD.chr12.log          EUR_CAD.chr17.log          EUR_CAD.chr21.log          EUR_CAD.chr5.log          
EUR_CAD.chr12.sscore       EUR_CAD.chr17.sscore       EUR_CAD.chr21.sscore       EUR_CAD.chr5.sscore       
EUR_CAD.chr12.sscore.vars  EUR_CAD.chr17.sscore.vars  EUR_CAD.chr21.sscore.vars  EUR_CAD.chr5.sscore.vars  
EUR_CAD.chr13.log          EUR_CAD.chr18.log          EUR_CAD.chr22.log          EUR_CAD.chr6.log          
EUR_CAD.chr13.sscore       EUR_CAD.chr18.sscore       EUR_CAD.chr22.sscore       EUR_CAD.chr6.sscore       
EUR_CAD.chr13.sscore.vars  EUR_CAD.chr18.sscore.vars  EUR_CAD.chr22.sscore.vars  EUR_CAD.chr6.sscore.vars  
EUR_CAD.chr14.log          EUR_CAD.chr19.log          EUR_CAD.chr2.log           EUR_CAD.chr7.log
EUR_CAD.chr14.sscore       EUR_CAD.chr19.sscore       EUR_CAD.chr2.sscore        EUR_CAD.chr7.sscore
EUR_CAD.chr14.sscore.vars  EUR_CAD.chr19.sscore.vars  EUR_CAD.chr2.sscore.vars   EUR_CAD.chr7.sscore.vars

分数文件内容

head EUR_CAD.chr1.sscore
#FID    IID     ALLELE_CT       NAMED_ALLELE_DOSAGE_SUM SCORE1_AVG      SCORE1_SUM
HG00096 HG00096 1046    486     0.00757595      7.92444
HG00097 HG00097 1046    484     0.00783352      8.19386
HG00099 HG00099 1046    505     0.00798495      8.35226
HG00101 HG00101 1046    491     0.00791584      8.27997
HG00102 HG00102 1046    474     0.00769178      8.04561
HG00103 HG00103 1046    502     0.00799328      8.36097
HG00105 HG00105 1046    500     0.00793847      8.30364
HG00107 HG00107 1046    468     0.00770316      8.0575
HG00108 HG00108 1046    469     0.00732639      7.66341

分染色体的计算的目的是，实际操作中，通常会使用巨大的pgen或bgen进行计算，合并文件并不现实, 这是一般需要分染色体计算并手动求和：

for chr in $(seq 1 22)
do
plink2 \
    --pfile chr${chr} \
    --score ${score} 1 2 3 header list-variants cols=+scoresums \
    --out chr${chr}
done

第二步 将各个染色体的结果提取 step2 extract raw scores into a single file

scoreFile=EUR_CAD

count=1
for chr in $(seq 1 22)
do
    file=${scoreFile}.chr${chr}.sscore
    if [ -s "$file" ] ; then 
        if [ ${count} -eq 1 ] ;then
        echo "ID        chr${chr}" > ./${scoreFile}.chrALL.score
        awk 'NR>1{print $1,$6}' ./${file} >> ./${scoreFile}.chrALL.score
        else
        paste ./${scoreFile}.chrALL.score <(cut -f6 ./${file} | awk -v chr=chr${chr} 'NR==1 {$0=chr} 1') >./${scoreFile}.temp&&mv ./${scoreFile}.temp ./${scoreFile}.chrALL.score
        fi
        count=`expr $count + 1`
     fi
done

所得文件

head EUR_CAD.chrALL.score
ID      chr1    chr2    chr3    chr4    chr5    chr6    chr7    chr8    chr9    chr10   chr11   chr12   chr13   chr14   chr15   chr16   chr17   chr18   chr19   chr20       chr21   chr22
HG00096 7.92444 6.41628 4.9392  3.9937  5.08024 7.50241 4.61922 3.59464 4.24131 4.56312 5.03334 5.55227 2.95436 2.32917 3.39488 3.61625 3.40913 2.02032 1.95575 2.74394     0.79493 1.33408
HG00097 8.19386 6.33598 5.0713  4.0514  4.92887 7.30242 4.19193 3.66247 4.514   4.42716 5.26378 5.11748 2.7589  2.47905 3.82365 3.83448 3.44519 2.09788 1.80506 2.7079      0.811121        1.27481
HG00099 8.35226 6.61542 5.199   3.94708 4.88824 7.72775 4.31098 3.58159 4.30785 4.81232 5.2327  6.05063 2.8803  2.3651  3.36827 3.54378 3.29725 2.08449 1.88188 2.52587     0.767397        1.21001
HG00101 8.27997 6.13397 5.36465 4.04592 4.88809 7.86323 4.49118 3.60872 4.27056 4.6258  5.42121 5.26046 2.70375 2.52093 3.56581 3.45794 3.30534 2.1327  1.70916 2.66579     0.818805        1.3808
HG00102 8.04561 6.32975 5.20324 3.86051 4.67724 7.78206 4.69662 3.38095 4.40059 4.67174 5.2312  5.04913 2.69084 2.48935 3.62454 3.61557 3.3044  2.12043 1.96028 2.82496     0.808453        1.46265
HG00103 8.36097 6.1202  5.31402 4.24136 4.91736 7.34715 4.55809 3.60716 4.15705 4.66235 5.04477 5.53387 2.70537 2.36537 3.76842 3.64108 3.33273 2.11081 2.00393 2.68089     0.763437        1.32735
HG00105 8.30364 6.13937 5.15716 4.19656 5.06392 7.8889  4.33995 3.78158 4.24975 4.58436 5.32105 5.72797 2.84577 2.43968 3.39822 3.60722 3.44641 1.9986  1.775   2.7736      0.793725        1.41736
HG00107 8.0575  6.51259 5.19973 4.06067 4.78711 7.14954 4.66686 3.81154 4.42637 4.45144 5.26257 5.46242 2.82289 2.28362 3.33811 3.58244 3.25041 2.11758 2.00922 2.70618     0.917279        1.43502
HG00108 7.66341 6.18669 4.98761 4.05088 4.7294  7.39041 4.08688 3.53173 4.43728 4.80822 5.02485 5.52436 3.12156 2.35199 3.54311 3.49076 2.97043 2.12883 1.91326 2.51056     0.817221        1.47096

第三步 将分数进行简单加和 step3 combine the scores using awk

scoreFile=EUR_CAD
#sum the scores from each chr
awk 'BEGIN{t=0}
        {if(NR==1){
                print "ID","score"
                  }
                else{
                        for(i=2;i<=NF;i++) t+=$i 
                        print $1,t
                    }
        }' ./${scoreFile}.chrALL.score > ./${scoreFile}.summary.score

所得文件

head EUR_CAD.summary.score
ID score
HG00096 88.013
HG00097 176.112
HG00099 265.062
HG00101 353.577
HG00102 441.807
HG00103 530.37
HG00105 619.62
HG00107 707.931
HG00108 794.672

求和完成，获得了原始分数（没有进行任何操作，没有标准化，没有平均，只是所有variant的效应量与dosage乘积的和），可以用于后续PRS分析

参考：

https://www.cog-genomics.org/plink/2.0/score

https://www.pgscatalog.org/browse/scores/

https://choishingwan.github.io/PRS-Tutorial/plink/

多基因风险分数 PRS( Polygenic risk score)系列之八：PGS Catalog

本文内容：

  1. PGS Catalog 简介
  2. PGS Catalog的纳入标准
  3. 从PGS Catalog寻找PGS
  4. PGS分数文件格式与下载
  5. 下载PGS后使用PLINK计算PGS
  6. 参考

回顾：

PGS Catalog 简介

本文简要介绍PGS Catalog的基本信息与使用方法。该数据库对于未来的PGS相关研究可以说是必不可少的，或多或少都需要通过此数据库查询，下载已有的PGS或上传自己的PGS模型。

与 GWAS catalog 类似， PGS Catalog 是一个已发表多基因风险分数 （polygenic scores）的公开数据库。在PGS Catalog中的每个PGS都被统一地标注了相关的元信息：包括分数文件（variants, effect alleles/weights），PGS如何构建与应用的注释，以及其预测表现的评价等。PGS对应的表型会被连接到相应的EFO（Experimental Factor Ontology,https://www.ebi.ac.uk/efo/）以保持研究间的统一(GWAS catalog 也使用EFO)。

PGS Catalog旨在对PGS构建索引，并以标准化的形式分发每个PGS的关键信息（variants，结果，实验设计等），以促进对PGS分析有效性的评价。

该数据库由剑桥大学Michael Inouye（在推上很活跃的大佬，建议关注）组的Samuel Lambert与HDR UK及NHGRI-EBI （GWAS Catalog）合作开发。

PGS Catalog 的主页

PGS Catalog的纳入标准

纳入PGSCatalog的标准主要有两大块：

  1. 新近开发的PGS，包含其分数与预测能力的必要基础信息 （需要在独立样本中评估）
  2. 对已开发的PGS在新的群体中进行评估。

纳入后每一个PGS都被赋予了识别编号， 例如 PGS000001

从PGS Catalog寻找PGS

查询PGS时， 可以通过搜索框直接搜索关键词查询PGS，或是通过表型，发表的文献等方式浏览数据库中的PGS.

以breast cancer 为例，查询后可以看到数据库中目前有112个乳腺癌相关的PGS：

点击后，可以查看这些PGS的汇总信息:

可以通过ancestry对PGS进行过滤，列表中的ancestry distribution表示的是，所用样本群体中各个族裔的构成。

选取感兴趣的PGS后，可以点击进入查看详细信息，或是直接下载PGS模型文件。

每个PGS的页面包括了PGS的详细信息，构建方法与参数，原始GWAS数据，评价指标，评价时所用样本信息等等。

PGS分数文件格式与下载

PGS Catalog数据库中的文件格式说明可以参考：https://www.pgscatalog.org/downloads/

如下所示，Scoring File Format由两部分组成，header和数据。

Header部分主要为该文件版本信息，PGS的基础信息，以及原始研究的信息，数据部分则包括了variant和计算PGS的allele与权重，大多可以来直接使用。

###PGS CATALOG SCORING FILE - see <https://www.pgscatalog.org/downloads/#dl_ftp_scoring> for additional information
#format_version=2.0
##POLYGENIC SCORE (PGS) INFORMATION
#pgs_id=PGS000001
#pgs_name=PRS77_BC
#trait_reported=Breast Cancer
#trait_mapped=breast carcinoma
#trait_efo=EFO_0000305
#weight_type=NR
#genome_build=NR
#variants_number=77
##SOURCE INFORMATION
#pgp_id=PGP000001
#citation=Mavaddat N et al. J Natl Cancer Inst (2015). doi:10.1093/jnci/djv036
rsID	chr_name	effect_allele	other_allele	effect_weight	locus_name	OR
rs78540526	11	T	C	0.16220387987485377	CCND1	1.1761
...

下载PGS后使用PLINK计算PGS

确认基因组版本等信息无误后，结合手头的基因型数据，可以通过PLINK来计算PGS。（与手头基因型文件的variant ID不一致时需要重新匹配）

https://www.cog-genomics.org/plink/2.0/score 或 GWASLab：多基因风险分数 PRS( Polygenic risk score)系列之二：使用PLINK计算PRS（C+T方法）的后半部分介绍了计算方法。

plink2 --score <filename> [i] [j] [k] [{header | header-read}]
                   [{center | variance-standardize | dominant | recessive}]
                   ['no-mean-imputation'] ['se'] ['zs'] ['ignore-dup-ids']
                   [{list-variants | list-variants-zs}]
                   ['cols='<column set descriptor>]

需要注意的是，有时我们手里的插补后的dosage文件是分染色体的，而PGS模型文件通常包括所有染色体上的variants，这种情况下一般需要分染色体进行计算单纯的分数加和 （使用—score里的cols=+scoresums 选项），然后再把22条染色体的分数再次加和算得总分数。

PLINK2 score的输出文件表头

Header	Column set	Contents
FID	maybefid, fid	Family ID
IID	(required)	Individual ID
SID	maybesid, sid	Source ID
PHENO1	pheno1	All-missing phenotype column, if none loaded
<Pheno name>, ...	pheno1, phenos	Phenotype value(s) (only first if just 'pheno1')
ALLELE_CT	nallele	Number of alleles across scored variants
DENOM	denom	Denominator used for score average
NAMED_ALLELE_DOSAGE_SUM	dosagesum	Sum of named allele dosages
<Score name>_AVG, ...	scoreavgs	Score averages
<Score name>_SUM, ...	scoresums	Score sums #分染色体时使用这一列求和

参考

https://www.pgscatalog.org/

Samuel A. Lambert, Laurent Gil, Simon Jupp, Scott C. Ritchie, Yu Xu, Annalisa Buniello, Aoife McMahon, Gad Abraham, Michael Chapman, Helen Parkinson, John Danesh, Jacqueline A. L. MacArthur and Michael Inouye.

The Polygenic Score Catalog as an open database for reproducibility and systematic evaluation

Nature Geneticsdoi: 10.1038/s41588-021-00783-5 (2021).

https://www.ebi.ac.uk/efo/

多基因风险分数 PRS( Polygenic risk score)系列之五：使用PRS-CS计算PRS（beta-shrinkage方法）

本文内容

  1. PRS系列回顾
  2. PRS-CS简介
  3. 概念框架
  4. 使用方法
  5. 参考

系列回顾：

PRS-CS简介

本文将介绍一种使用GWAS数据与外部LD参考面板来计算SNP后验效应量的方法， PRS-CS。

该方法利用了高维贝叶斯回归的框架，与之前类似研究最大的不同点便是对于beta使用了连续收缩（continuous shrinkage， CS）先验分布，适应更多样的遗传结构，并大幅提高了计算效率，使局部LD特征的多变量建模成为可能。

概念框架

  1. 考虑一个贝叶斯高维回归框架
  2. 常用的beta的先验分布通常可以表示为多个正态分布的比例混合
  3. 为了构建更为灵活的模型以更好反映遗传结构，一些方法采用了两个或多个质点或分布的离散混合，相比单纯的正太先验分布，这类方法通常能够构建更广的效应量分布。例如LDpred。
  4. 但此类方法后验推断需要极大的计算量，可能不能准确的建模出局部的LD结构。
  5. 为了解决这些问题，PRS-CS的作者采用了一种与先前离散混合概念不同的先验分布，也就是连续收缩先验分布，也就是正态分布的全局-局部比例混合
  6. PRS-CS对于全局比例系数采取两种不同算法进行估计。一是搜索固定的系数，而是通过指定全局系数的先验分布来在给定数据中进行估计。

详细推导请参考原论文：T Ge, CY Chen, Y Ni, YCA Feng, JW Smoller. Polygenic Prediction via Bayesian Regression and Continuous Shrinkage Priors. Nature Communications, 10:1776, 2019.

使用方法

PRS-CS由Python语言写成，是python2与3同时兼容的。需要安装scipy与h5py这两个包。

PRS-CS 本体与外部LD参考面板的下载：

https://github.com/getian107/PRScs

git clone <https://github.com/getian107/PRScs.git>

下载完成后，检验是否安装成功：

./PRScs.py --help

下载对应人群的LD参考面板，作者提供了千人基因组以及UKB数据的参考面板：

https://github.com/getian107/PRScs#getting-started

输入准备

  1. 上面下载的LD参考面板 plink格式
  2. 目标群体的bim文件：该文件只是用来提供target数据集中的SNP列表
  3. GWAS sumstats

sumstats的格式如下

SNP          A1   A2   BETA      P
rs4970383    C    A    -0.0064   4.7780e-01
rs4475691    C    T    -0.0145   1.2450e-01
rs13302982   A    G    -0.0232   2.4290e-01

或是

SNP          A1   A2   OR        P
rs4970383    A    C    0.9825    0.5737                 
rs4475691    T    C    0.9436    0.0691
rs13302982   A    G    1.1337    0.0209
...

注意A1是effect allele， A2是non-effect allele

PRS模型计算

使用方法如下

python PRScs.py \
  --ref_dir=PATH_TO_REFERENCE \ # LD参考面板的文件夹路径
  --bim_prefix=VALIDATION_BIM_PREFIX \ #目标群体plink的bim格式文件的路径
  --sst_file=SUM_STATS_FILE \  # GWAS sumstats的路径
  --n_gwas=GWAS_SAMPLE_SIZE \ # GWAS的样本量大小
  --out_dir=OUTPUT_DIR  #输出文件夹

#以下为可选项
  #--a=PARAM_A  \ gamma-gamma prior中的参数a，默认为1
  #--b=PARAM_B  \ gamma-gamma prior中的参数b，默认为0.5
  #--phi=PARAM_PHI \ 全局比例系数，不指定时自动估计（PRS-CS-auto），也可以小规模网格搜索（phi=1e-6, 1e-4, 1e-2, 1）
  #--n_iter=MCMC_ITERATIONS \ MCMC迭代次数，默认1000
  #--n_burnin=MCMC_BURNIN \ MCMC中burnin的次数，默认500
  #--thin=MCMC_THINNING_FACTOR \ 马尔科夫链的thinning factor，默认为5
  #--chrom=CHROM \ 可以只单独计算一条染色体
  #--beta_std=BETA_STD \ 若为True，则输出标准化的后验SNP效应量 
  #--seed=SEED 随机数种子

PRS-CS使用scipy，会自动占用所有可用的cpu核心，使用服务器时可能会出现干扰，可以通过以下shell脚本指定使用核心数：

export MKL_NUM_THREADS=$N_THREADS
export NUMEXPR_NUM_THREADS=$N_THREADS
export OMP_NUM_THREADS=$N_THREADS

例如，只用一个核时，N_THREADS=1

输出结果

输出文件包含五列，rsID，碱基位置，A1，A2 与后验效应量估计值

然后使用该文件和plink可以对目标人群计算PRS： https://www.cog-genomics.org/plink/1.9/score

分染色体计算时，最后加和各个染色体的PRS即可

测试例子

使用eur的参考面板与test_data文件夹里的gwas数据，以及一个有22号染色体上1000个SNP的bim文件：

python PRScs.py \
--ref_dir=path_to_ref/ldblk_1kg_eur \
--bim_prefix=path_to_bim/test \
--sst_file=path_to_sumstats/sumstats.txt \
--n_gwas=200000 \
--chrom=22 \
--phi=1e-2 \
--out_dir=path_to_output/eur

参考

T Ge, CY Chen, Y Ni, YCA Feng, JW Smoller. Polygenic Prediction via Bayesian Regression and Continuous Shrinkage Priors. Nature Communications, 10:1776, 2019.

rsID的介绍与chr:pos转换时的陷阱

很多小伙伴都觉得位置转换rsID是很麻烦的事情，有时会偷懒只用手头文件的chr:pos位置信息匹配rsID，但这样做带来的的问题却少有人讨论，本文将主要介绍什么是rsID，以及rsID在使用和转换中的一些常见问题。

本文内容
什么是rsID
主要优点
rsID可能表示的变异类型
（重点）rsID与chrpos转换时的常见错误
解决办法
参考

什么是rsID

rsID 就是 dbSNP的Reference SNP ID （缩写为rs 或者RefSNP），一个由dbSNP设定的，为了识别变异位点的一串数字编号。rsID设计上是非冗余的，也就是全局唯一的id，用户提交的变异会被归类整理注释，重复的变异会被整合。

主要优点

rsID无关参考基因组版本，不像chrpos会随版本变化而变化, rsID在不同版本间是一致的。对于群体遗传学或是精准医学的大规模的研究来说会更加方便，rsID提供了稳定的变异表示方法。（摘自官网，个人认为有时候rsID的转换带来的问题远超不转换的问题，有好有坏，但是传统上还是需要转换）

rsID表示变异的类型

rsID中的rs尽管是Reference SNP的首字母缩写，但实际上一些其他类型的变异也会被赋予rsID。（通常变异的长度小于50bp）

  • 单核苷酸变异 Single nucleotide variation (SNV)
  • 短多核苷酸变异 Short multi-nucleotide changes (MNV)
  • 较小的短插入或删除 Small deletions or insertions (INDEL)
  • 较小的短串联重复序列 Small STR repeats
  • 逆转录转座子插入 retrotransposable element insertions

rsID是把双刃剑：仅凭chr：pos与rsID互相转换时的陷阱

  • 仅使用chr:pos 转换 rsID时的问题：
  1. 对应位点rsID不存在，可能是新变异等等原因，通常可以以chr:pos:ref:alt的形式替代。但还有个问题就是Alt allele不存在，比如rs123456 对应chr1：123456的 T>C,A 而你手里的数据是chr1：123456的 T>G， 那问题来了，这应不应该给他们相同的rsID？仅凭位点和类型来说应该给，或许下个版本的dbsnp会加上这个变异，但其实我也没有明确的答案（欢迎评论区讨论），不过实际操作中我会倾向于保守一点，用chr:pos:ref:alt 而不是rsID来表示。
  2. 如上rsID的介绍所述，rsID并不止只用来表示单一核苷酸的SNP，也会表示其他变异类型，这会导致同一位点有多个rsID表示的变异，最常见的就是某个位点同时有SNP和INDEL，仅凭chr:pos信息而不管allele的话会混淆并大量的错误匹配SNP与INDEL的rsID，后续功能分析会引起很大的不便，举个例子： rs123456 对应chr1：123456的 T>C ,而rs987654 同样对应chr1：123456这个位置，但是这个变异是个INDEL， T>TA， 如果仅凭chr：pos匹配会混淆SNP与INDEL，虽然是同样的位置，但变异造成的影响会完全不同。解释时本应是rs987654这个INDEL造成的影响却错误地解释到rs123456这个SNP上，这种情况应该被避免。这么做破坏了rsID的唯一性特点，是不是有点违背初衷，本末倒置了。
  3. 还有一个问题就是手头数据里的变异是否已经标准化？ 未标准化的变异的chrpos是不准确的，进行左对齐与节俭原则的标准化后可能产生位移，用未标准化chrpos匹配时可能会错位匹配到其他相邻的位点上。比如手头的变异可能是 chr1:123456:AA:AT ,标准化后则是chr1:123457:A:T，向后移了一位，如果你看过1000genome的原始数据就会发现这样的情况大量存在，所以应当注意（参考：GWASLab：变异的标准化 Variant Normalization）
  4. 0起点还是1起点的参考系问题，处理数据时应该注意，这里不做过多赘述。（GWASLab：LiftOver 基因组坐标变换 与 01坐标系统）

rsID 向 chr：pos 某参考基因组版本的位置转换时，会遇到的问题：

  1. 设计上rsID是唯一对应某个变异的，但实际上由于dbSNP版本的不同或其他原因，手头GWAS的sumstats里的rsID可能对应两个位置， 而多个rsID又可能对应同一个位置上相同的变异
  2. 在对应参考基因组版本上的位置不存在等等

解决办法

rsID转换chrpos时要尽量明确原始数据的dbsnp版本，能确定版本的时候用对应版本，不能的时候要制定统一标准（为了研究的可重复性），转换时要使用统一的dbsnp的版本。

而chrpos转换rsID时，不贪多，不求快，老老实实用先确认标准化，然后利用注释的方法，也就是相应基因组版本的 位置chr:pos以及 ref与alt全部与rsID全部匹配时才进行转换。

可以参考以下内容：

GWASLab：使用ANNOVAR对变异进行功能注释

GWASLab：SNP的rsID与位置信息的相互匹配 rsID/ chr:pos conversion

参考：

https://www.ncbi.nlm.nih.gov/snp/do

使用LDSC计算LD分数 – LD score

目录

基于PLINK文件计算LD分数
LD分数文件格式
用于LDSC-SEG的分层LD分数的计算

有很多时候没有现成的LD分数参考，而需要我们自己根据手头基因型数据而计算LD分数（例如一个常用的例子是GWAS数据与scRNA数据的结合 – 使用自己的scRNA数据提取特征基因后计算LD分数并进行partitioned LD 分数回归以检测细胞特异性）。

本文将简要介绍如何计算 单变量的LD分数 以及 分层的LD分数。

回顾：

  1. GWASLab：连锁不平衡分数回归 LD score regression -LDSC
  2. GWASLab：通过Bivariate LD Score regression估计遗传相关性 genetic correlation
  3. GWASLab：基于功能分类分割遗传力 – 分层LD分数回归 Stratified LD score regression
  4. GWASLab：使用GWAS数据进行组织细胞特异性分析 – LDSC-SEG

使用LDSC计算单变量LD分数

单变量LD分数为最基本的LD分数的形式，常用在ldsc -h2选项的参考LD分数中。

输入文件： PLINK的 bed / bim / fam文件

使用软件： ldsc

这里推荐使用千人基因组相应族裔的数据（vcf格式），可通过plink -vcf转化为plink格式。

计算LD分数时需要指定窗口的大小，作者推荐 1 centiMorgan (cM) window

一般情况下plink格式中 表示cM的列都为零，可以使用plink —cm-map以及额外的遗传图谱文件来填补bim文件中的cM列

（从ldsc网站下载的plink文件中bim文件的cM列已经被填补，可以直接使用）

下面简单演示如何计算：

示例数据为千人基因组欧洲人群的第22号染色体：

wget <https://data.broadinstitute.org/alkesgroup/LDSCORE/1kg_eur.tar.bz2>
tar -jxvf 1kg_eur.tar.bz2

22.bim
22.fam
22.bed
22.hm3.daf.gz

可以通过以下的代码来计算ld分数 （-l2 选项）

python ldsc.py \
	--bfile ${plinkfile} \           #指定plink文件路径及前缀
	--l2 \                         #计算ld分数
	--ld-wind-cm 1 \                 #指定窗口的大小，单位为cM
	--out 22                         #输出文件的前缀

执行上述代码后得到如下四个文件：

22.log
22.l2.M
22.l2.M_5_50
22.l2.ldscore.gz

LD分数相关文件格式

下面简要介绍LD分数文件的相关格式，主要的输出包括以下五种文件：

.log
.l2.ldscore
.annot
.l2.M_5_50
.l2.M

.log LD分数计算后得到的日志文件，其中会包含LD分数的总结性数据，例如：

Summary of LD Scores in 22.l2.ldscore.gz
      MAF     L2
mean  0.232   18.535
std   0.145   16.104
min   0.001    0.066
25%   0.104    7.839
50%   0.224   13.484
75%   0.355   22.972
max   0.500  109.716

MAF/LD Score Correlation Matrix
     MAF    L2
MAF  1.000  0.275
L2   0.275  1.000
Analysis finished at Fri Jan 30 10:58:46 2015
Total time elapsed: 2.72s

存储LD分数最主要的文件：

.l2.ldscore 文件

包含3+N列，N≥1, 前3列分别为

  1. CHR — chromosome 染色体号
  2. SNP — SNP identifier (rs number) rsID
  3. BP — physical position (base pairs) 物理位置

第三列以后为LD分数的列，可以有多列，对应不同的注释组

  1. all additional columns — LD Scores
CHR SNP	        BP	        L2
22	rs9617528	16061016	1.271
22	rs4911642	16504399	1.805
22	rs140378	16877135	3.849
22	rs131560	16877230	3.769
22	rs7287144	16886873	7.226
22	rs5748616	16888900	7.379
22	rs5748662	16892858	7.195
22	rs5994034	16894090	2.898
22	rs4010554	16894264	6.975

.annot注释文件

上面单变量LD分数的计算中我们使用的是plink文件里所有的SNP，未使用到注释文件，但后续分层LD分数计算时，我们需要用到annot文件，来注释计算LD分数时使用的SNP

该文件每行对应一个SNP，空格分隔，有表头，需要按以下顺序排列：

  1. CHR — chromosome 染色体号
  2. BP — physical position (base pairs) 物理位置
  3. SNP — SNP identifier (rs number) rsID
  4. CM — genetic position (centimorgans) 遗传距离
  5. all additional columns — Annotations 一列或多列注释

注释列既可以为0/1二分类，也可是连续的。

例如 Example:

CHR BP SNP CM AN1 AN2
1   1  rs1  0  1  0
1   2  rs2  0  1  0
1   3  rs3  0  0  1

最后则是两个辅助文件：

.l2.M_5_50

该文件只有一行，列数对应着.l2.ldscore文件中annotation中列的个数，并与其顺序一致。

每一列的数字则表示对应的注释分类中MAF>5%的SNP的个数。

（没有附加注释文件时就是该染色体上全部MAF>5%的SNP数量）

.l2.M

与l2.M_5_50相同，只是没有MAF的限制，即表示对应注释总的SNP数

例如：（对应两个annotation分类）

100	1000

计算分层LD分数

通过某种方式，选取注释组中包含的基因

例如使用单细胞测序中某个细胞特异表达的前10%的基因等，

注意：目前ldsc只支持常染色体。

为了计算某种注释特有的LD分数，需要准备一个.annot的注释文件，格式如上所述。

这个注释里的位点的顺序应该与.bim文件中的SNP完全相同。ldsc也允许—thin-annot 格式，也就是上述annot文件忽略掉CHR,BP,SNP以及CM列。

下面介绍如何构建annot文件并以此计算相应注释的LD分数：

Step 1: Creating an annot file 第一步，构建注释文件

输入文件：

—gene-set-file：注释包含的基因集

head GTEx_Cortex.GeneSet
ENSG00000105605
ENSG00000169862
ENSG00000074317
ENSG00000196361
ENSG00000221946

–gene-coord-file：基因坐标文件

head ENSG_coord.txt
GENE	CHR	START	END
ENSG00000243485	chr1	29554	31109
ENSG00000237613	chr1	34554	36081
ENSG00000186092	chr1	69091	70008
ENSG00000238009	chr1	89295	133566
ENSG00000239945	chr1	89551	91105

–windowsize：基因上下游LD计算时所包含窗口大小

–bimfile：计算LD所用PLINK文件中的bim文件

head 1000G.EUR.QC.22.bim 
22	rs587616822	-0.0048996974	16050840	G	C
22	rs62224609	-0.00094708154	16051249	C	T
22	rs587646183	0.010833912	16052463	C	T
22	rs139918843	0.012979739	16052684	C	A
22	rs587743102	0.014465964	16052837	T	C

–annot-file：输出文件

所使用的代码如下所示：使用lsmake_annot.py

python make_annot.py \
		--gene-set-file GTEx_Cortex.GeneSet \
		--gene-coord-file ENSG_coord.txt \
		--windowsize 100000 \
		--bimfile 1000G.EUR.QC.22.bim \
		--annot-file GTEx_Cortex.annot.gz

也可以直接使用bed文件计算

python make_annot.py \
		--bed-file Brain_DPC_H3K27ac.bed \
		--bimfile 1000G.EUR.QC.22.bim \
		--annot-file Brain_DPC_H3K27ac.annot.gz

结果如下：

zcat GTEx_Cortex.annot.gz | head
ANNOT
0
0
0
0
0

Step 2: Computing LD scores with an annot file. 第二步，使用注释文件计算LD分数

使用第一步计算所得的.annot文件（忽略掉了CHR,BP,SNP以及CM列，所以使用–thin-annot选项）

–print-snps hm.22.snp：只打印包含在hm.22.snp的SNP

python ldsc.py \
		--l2 \ 
		--bfile 1000G.EUR.QC.22 \
		--ld-wind-cm 1\
		--annot Brain_DPC_H3K27ac.annot.gz \
		--thin-annot \
		--out Brain_DPC_H3K27ac\
		--print-snps hm.22.snp

如果要与baseline model一起使用的话，要注意使用的SNP应该完全相同。

正式计算时只需要对所有染色体循环即可，确保输出都在同一个文件夹里，且有着相同的前缀，例如：

${prefix}.${chr}.annot.gz , ${prefix}.${chr}.l2.ldscore , and ${prefix}.${chr}.l2.M_5_50

这些文件可以用于后续分层LDSC回归分析中。

GWASLab：使用GWAS数据进行组织细胞特异性分析 – LDSC-SEG

参考

https://github.com/bulik/ldsc

使用GWAS数据估计跨族裔遗传相关 popcorn – Cross-ancestry genetic correlation

popcorn 背景介绍

回顾（在单一族裔中估计遗传相关的方法）：通过Bivariate LD Score regression估计遗传相关性 genetic correlation

随着GWAS等遗传变异关联研究在不同人群中不断开展，相关研究数量不断增加，这为我们提供了宝贵的机会以研究遗传结构在不同人种中的差异，有助于解决这个在医疗研究与群体遗传学中十分重要的问题。

该文章基于Brielin等的研究，简单介绍一种估计跨族裔遗传相关的方法，popcorn，用于估计在不同群体中常见SNP的因果效应量的相关性。该方法纳入了研究中所有SNP的关联信息（区别于其他需要事先进行LD-pruning的方法），而且仅使用GWAS的概括数据，减少了计算负担，并避免了无法获取基因型数据的问题。

通常情况下，在单一群体中，两个表性之间的遗传相关的定义为对于两个表型的SNP效应量大小之间的相关系数。而在多群体的情况时，因为不同群体内等位基因频率有显著差异，定义并不统一。因为某个变异可能在某个特定群体中有较高的效应量但较低的频率，所以本方法不仅考虑了效应量大小的相关，同时也考虑遗传冲击（allelic impact）的相关性。

该文中，跨族裔遗传效应相关的定义为SNP效应量的相关系数，跨族裔遗传冲击相关的定义为特定群体的等位方差正态化（allele-variance-normalized）的SNP效应量之间的相关系数。

直觉上，遗传效应相关性（genetic-effect correlation）衡量的是同一个SNP造成表型改变的程度差异，而遗传冲击相关性（genetic-impact correlation）则是分别在各个群体中，相比于的稀有allele，给予common allele更高的权重。举个例子，如果只看效应相关性，计算得出的相关系数是不完全的，没有反应出两个群体间的效应的完整信息，因为即使效应量的遗传相关是1，但其在两个群体中，对其各自表型分布的冲击也可能由于allele frequency的不同而不同。

所以跨族裔遗传相关的两个核心问题就被引出：

1 同一个变异在两个群体中效应量大小的差异？

2 同一个变异的效应量在两个群体中的差异是否被不同群体的allele frequency所稀释或加重？

为了估计遗传相关，popcorn采用了贝叶斯方法，假设基因型是分别从各个群体内抽取的，并且效应量服从正态的先验分布（无穷小模型）。无穷小模型的假设会产生一个观测统计量（Z scores）的多元正态分布，其中该分布的协方差是遗传力与遗传相关的一个方程。这使得我们可以直接将Z score的膨胀纳入模型中，而不需要进行LD pruning。然后popcorn会最大化近似加权似然方程，来估计遗传力与遗传相关性。

方程推导可参考原文章，这里我们要估计的是以下两个值：

遗传效应相关：pge=Cor(β1，β2)

遗传冲击相关：pgi=Cor(δ1β1，δ2β2)

其中δ为allele的标准差

使用方法：

该文章作者的github仓库： https://github.com/brielin/Popcorn

要求：

popcorn只能使用python2，建议用conda新建一个环境
需要以下python包：
numpy 1.14.2
scipy 1.0.1
pandas 0.22.0
pysnptools 0.3.9
bottleneck 1.0.0
statsmodels 0.8.0
(to use --plot_likelihood) matplotlib 1.5.1

从github clone之后，安装：

cd Popcorn
python setup.py install

可以下载使用千人基因组项目提前计算好的LD分数 （用于EUR-EAS）：

https://www.dropbox.com/sh/37n7drt7q4sjrzn/AAAa1HFeeRAE5M3YWG9Ac2Bta .

popcorn 方法分为两步，

第一步为计算LD分数（使用下载好的数据可以跳过这一步，作者提供了EUR-EAS的LD分数）

第二步为计算遗传相关性

第一步，计算LD分数（可选）

python -m Popcorn compute -v 2 --bfile1 Popcorn/test/EUR_ref --bfile2 Popcorn/test/EAS_ref --gen_effect Popcorn/test/EUR_EAS_test_ge.cscore

-v 表示 输出log的详细程度

—bfile表示 输入的plink bfile文件前缀

—gen_effec 表示计算遗传效应相关 （计算遗传冲击相关时不加这个flag）

最后是输出的路径和文件名

第一步log文件

Popcorn version 0.9.6
(C) 2015-2016 Brielin C Brown
University of California, Berkeley
GNU General Public License v3

Invoking command: python /home/brielin/CoHeritability/Popcorn/__main__.py compute -v 2 --bfile1 Popcorn/test/EUR_ref --bfile2 Popcorn/test/EAS_ref Popcorn/test/EUR_EAS_test.cscore
Beginning analysis at DATE
50000 SNPs in file 1
50000 SNPs in file 2
49855 SNPs in file 1 after MAF filter
44021 SNPs in file 2 after MAF filter
43898 SNPs common in both populations
T1
T2
TC
Analysis finished at DATE

结果的格式如下所示：

1	14930	rs75454623	A	G	0.520874751491	0.58630952381	1.4252539451	1.78489131664	1.49214493091
1	15211	rs78601809	T	G	0.731610337972	0.503968253968	1.20243142615	2.3876817626	1.29403313474
1	15820	rs200482301	T	G	0.728628230616	0.605158730159	1.56556914093	1.42934198599	1.40055911225
1	55545	rs28396308	T	C	0.813121272366	0.804563492063	2.59950434496	2.1809181648	2.06610287872

各列分别代表Chromosome, Base Position, SNP ID, Allele 1, Allele 2, Frequency of A1 in POP1, Frequency of A1 in POP2, LD score in POP1, LD score in POP2, and Cross-covariance score

第二步，计算相关

python -m Popcorn fit -v 1 --use_mle --cfile Popcorn/test/EUR_EAS_test_ge.cscore --gen_effect --sfile1 Popcorn/test/EUR_test.txt --sfile2 Popcorn/test/EAS_test.txt Popcorn/test/EAS_EUR_test_ge_result.txt

–sfile1与–sfile2为输入的两个群体的GWAS文件，注意要与LD分数中POP1和POP2的顺序相一致

输入的GWAS数据至少包含一下列（列名应与下面的介绍保持一致）：

1 rsid 或者 SNP （与LD分数文件中的id保持一致）

注： 可以使用 chr 以及 pos 来替代

2 a1 和 a2

3 N 每个SNP的样本大小

4 beta和SE 或者 OR和p-value 或者 Z分数 （不要求对应a1为effect allele，但要保持所有snp一致即可）

5 AF （可选）即a2的allele frequency，用于A/T ， G/C的SNP的flip

输入文件例如：

rsid	a1	a2	af	N	beta	SE
rs10458597	C	A	0.59421	50000	-0.0152782557183	0.00912151085515
rs3131972	A	C	0.83102	50000	-0.000638379272685	0.0119663325893
rs3131969	A	C	0.8654	50000	-0.000737906302463	0.0131325861467
rs3131967	A	C	0.87044	50000	-0.000189441590945	0.0133506462369

执行代码后的，第二步log文件：

Popcorn version 0.9.6
(C) 2015-2016 Brielin C Brown
University of California, Berkeley
GNU General Public License v3

Invoking command: python /home/brielin/CoHeritability/Popcorn/__main__.py fit -v 1 --cfile Popcorn/test/EUR_EAS_test_ge.cscore --gen_effect --sfile1 Popcorn/test/EUR_test.txt --sfile2 Popcorn/test/EAS_test.txt Popcorn/test/EAS_EUR_test_ge_result.txt
Beginning analysis at DATE
Analyzing a pair of traits in two populations
49999 49999 SNPs detected in input.
43897 SNPs remaining after merging with score file.
43897 SNPs remaining after filtering on AF and self-compliment SNPs.
Initial estimate:
       Val (obs)  SE
h1^2   0.172133 NaN
h2^2   0.086708 NaN
pg     0.302372 NaN
Performing jackknife estimation of the standard error using 200 blocks of size 219 .
Jackknife iter: 200
      Val (obs)        SE          Z     P (Z)
h1^2   0.172133  0.012870  13.374388      0
h2^2   0.086708  0.008555  10.135759      0
pge    0.302372  0.053021  13.157553      0
Analysis finished at DATE
Total time elapsed: T

pge 则为跨族裔遗传相关的估计值 (加–gen_effect时的结果)

pgi 为跨族裔遗传冲击的估计值（不加–gen_effect时的结果）

这里的p值的原假设是估计值等于1，p<0.05则意味着估计值显著小于1

参考：

https://pubmed.ncbi.nlm.nih.gov/27321947/

使用GWAS数据进行组织细胞特异性分析 – LDSC-SEG

目录

LDSC-SEG简介
LDSC-SEG原理
LDSC-SEG教程
参考

LDSC-SEG简介

本文主要介绍LD分数回归的一项功能扩展 ，LDSC-SEG。该方法主要通过整合基因表达数据与GWAS数据，来发现疾病相关的组织或细胞种类，其底层原理是使用分层LD分数回归（stratified LD score regression，回顾：GWASLab：基于功能分类分割遗传力 – 分层LD分数回归 Stratified LD score regression）来检测表型的遗传性是否富集于某个组织或细胞高特异表达基因的周围。

LDSC-SEG原理

LDSC-SEG的主要步骤 (如图所示)

  1. 从一个标准化后的基因表达矩阵（包含不同组织与细胞）开始
  2. 对于每个gene，首先计算其在目标组织中特异表达的t统计量
  3. 根据t统计量从大到小对所有基因进行排序，并将位于t统计量最高的前10%的基因定义为该组织特异表达的基因集。
  4. 在这些特异表达的基因的转录区域两侧加上100kb的窗口，并以此为构建组织特异的基因组注释。
  5. 最后对于以上注释后的不同组别进行分层LD回归来估计不同组织或细胞对于所研究表型遗传力的贡献

联合回归模型中同时包括

1）上述目标组织或细胞特异的基因集，

2）一个包含基因组上所有基因的基因集，

3）包含52种注释的基线模型（这些注释包括增强子区域，保守性区域等，可参考 stratified LD score regression）。

特异基因集的回归系数为正数，则表示矫正其他基因集后，该特异基因集对表型遗传性的贡献为正。

基因表达数据来源（原文中处理了五组公开的数据集，如下所示）

GTExHuman53 tissues/cell typesRNA-seq
Franke labHuman/mouse/rat152 tissues/cell typesArray
CahoyMouse3 brain cell typesArray
PsychENCODEHuman2 neuronal cell typesRNA-seq
ImmGenMouse292 immune cell typesArray

实战操作

ldsc 下载安装可参考： GWASLab：连锁不平衡分数回归 LD score regression -LDSC

教程原文：

https://github.com/bulik/ldsc/wiki/Cell-type-specific-analyses

#以上述5组数据中的Cahoy数据为例：
cts_name=Cahoy 

#下载对应的LD分数文件 （EUR）

#组织、细胞特异LD分数
wget https://data.broadinstitute.org/alkesgroup/LDSCORE/LDSC_SEG_ldscores/${cts_name}_1000Gv3_ldscores.tgz
#基线模型文件
wget https://data.broadinstitute.org/alkesgroup/LDSCORE/1000G_Phase3_baseline_ldscores.tgz
#权重文件
wget https://data.broadinstitute.org/alkesgroup/LDSCORE/weights_hm3_no_hla.tgz

#解压
tar -xvzf ${cts_name}_1000Gv3_ldscores.tgz
tar -xvzf 1000G_Phase3_baseline_ldscores.tgz
tar -xvzf weights_hm3_no_hla.tgz

#下载GWAS数据
wget https://data.broadinstitute.org/alkesgroup/UKBB/body_BMIz.sumstats.gz
#下载SNP list
wget https://data.broadinstitute.org/alkesgroup/LDSCORE/w_hm3.snplist.bz2
#解压
bunzip2 w_hm3.snplist.bz2

#第一步清洗数据 
python munge_sumstats.py \
--sumstats body_BMIz.sumstats.gz \
--merge-alleles w_hm3.snplist \
--out UKBB_BMI

#第二步 进行LDSC-SEG
cts_name=Cahoy
ldsc.py \
    --h2-cts UKBB_BMI.sumstats.gz \
    --ref-ld-chr 1000G_EUR_Phase3_baseline/baseline. \
    --out BMI_${cts_name} \
    --ref-ld-chr-cts $cts_name.ldcts \
    --w-ld-chr weights_hm3_no_hla/weights.

注意：

**--ref-ld-chr-cts 这里输入一个ldcts文件，共两列，第一列为一个便于识别的label，第二列则是逗号分隔的两个路径，第一个为被检测组织细胞的ld，第二个则为control的ld，路径格式与--ref-ld-chr的格式类似。注意这里的都是相对与解压文件夹的相对路径，使用前最好修改为绝对路径。

如下图所示：

#组织细胞标签 检验组LD分数路径,对照组LD分数路径
Astrocyte       Cahoy_1000Gv3_ldscores/Cahoy.1.,Cahoy_1000Gv3_ldscores/Cahoy.control.
Oligodendrocyte Cahoy_1000Gv3_ldscores/Cahoy.2.,Cahoy_1000Gv3_ldscores/Cahoy.control.
Neuron  Cahoy_1000Gv3_ldscores/Cahoy.3.,Cahoy_1000Gv3_ldscores/Cahoy.control.

执行完成后可以查看结果：

.cell_type_results.txt

Name    Coefficient     Coefficient_std_error   Coefficient_P_value
Neuron  7.93194788527e-09       3.02894244784e-09       0.00441303625204
Oligodendrocyte 7.32019970874e-10       3.51868270994e-09       0.417599619801
Astrocyte       -5.76220451287e-09      2.60400594455e-09       0.98654507806

第一列即为dict文件里的label，第二，三列为ldcts文件里第二例第一个路径对应的ld分数的系数与se（对应cell type specific annotation），第四列为该系数的p值。

参考

https://github.com/bulik/ldsc/wiki/Cell-type-specific-analyses

https://www.ncbi.nlm.nih.gov/pmc/ar

一行python画Manhattan plot与QQ plot

之前介绍过曼哈顿图与QQ图的画法，但自己画终究还是有点麻烦，有很多数据的时候就很头疼，于是自己写了一个非常简单的python package，一行代码画好对齐的Manhattan plot 与 QQ plot，并基于一个给定的滑动窗口自动检测top SNP并注释。

Package： gwaslab

安装方法： pip install gwaslab

使用方法：myplot = gl.mqqplot(insumstats,"CHR","POS","PVALUE")

当前版本：0.0.5

依赖的包：scipy,numpy,matplotlib,pandas,seaborn

（注意：非专业开发人员，完全用爱发电，自用的scripts改成的包，难免有bug，欢迎在github上指正，或提意见或建议， https://github.com/Cloufield/gwaslab ）

使用示例：

实例数据下载： http://jenger.riken.jp/result

ID 1 Atrial Fibrillation

读入数据

输入文件是一般的gwas sumstats就可以，有chr，pos，pvalue三列就可以画：

import pandas as pd
import gwaslab as gl

#读取输入文件
insumstats = pd.read_csv("AF_1000G_rsq09_FINAL.txt.gz","\\s+")

本次使用的示例数据如下

使用mqqplot函数画图：

输入gwas sumstats的DataFrame，并指定染色体，碱基位置，p值的列名即可：

myplot = gl.mqqplot(insumstats,"CHR","POS","PVALUE")

#log
Basic settings:
  - Genome-wide significance level is set to 5e-08 ...
  - Raw input contains 5018048 variants...
Start conversion and QC:
  - P values are being converted to -log10(P)...
  - Sanity check: 0 variants with P value outside of (0,1] will be removed...
  - Sanity check: 0 na/inf/-inf variants will be removed...
  - Maximum -log10(P) values is 134.014573525917 .
Plotting 5018048 variants:
  - Found 14 significant variants with a sliding window size of 500 kb...
  - Skip annotating
  - Created Manhattan plot successfully!
  - Created QQ plot successfully!

lambda gc 自动计算并注释， qq plot与manhattan plot的y轴对应，，看着是舒服一点了，

可是突出的那个loci太高，其他的loci都快看不见了，有点不协调啊，显著的loci也没有注释，怎么办？

那么加几个option好了：

1.用cut 截断一下，cut以上的轴按cutfactor成比例缩小，这样就能在不丢失信息的情况下看清所有显著的loci

2.anno选项是用来自动注释lead snp的，默认基于一个500kb的滑动窗口，可以通过windowsize改变

gl.mqqplot(insumstats,"CHR","POS","PVALUE",cut=20,cutfactor=20,anno=True)

#log
Basic settings:
  - Genome-wide significance level is set to 5e-08 ...
  - Raw input contains 5018048 variants...
Start conversion and QC:
  - P values are being converted to -log10(P)...
  - Sanity check: 0 variants with P value outside of (0,1] will be removed...
  - Sanity check: 0 na/inf/-inf variants will be removed...
  - Maximum -log10(P) values is 134.014573525917 .
  - Minus log10(P) values above 20 will be shrunk with a shrinkage factor of 20...
Plotting 5018048 variants:
  - Found 14 significant variants with a sliding window size of 500 kb...
  - Annotating using column CHR:POS...
  - Created Manhattan plot successfully!
  - Created QQ plot successfully!

嗯嗯，看着舒服多了，

如果 只指定anno=True, 那么注释就只是chr： pos，当然也可以指定用于注释的列名，这里用SNP这一列注释：

gl.mqqplot(insumstats,"CHR","POS","PVALUE",cut=20,cutfactor=20,anno="SNP")

颜色不好看怎么办：

用colors选项，传个颜色的list进去，给图换个颜色，

qqplot的颜色，为了保持视觉统一，设定为曼哈顿图chr1的颜色,

例如传个彩虹进去：

myplot = gl.mqqplot(insumstats,"CHR","POS","PVALUE",
                    cut=20,cutfactor=20,anno=True,
                    colors=["#ff0000","#fc4444","#fc6404","#fcd444","#8cc43c","#029658","#1abc9c","#5bc0de","#6454ac","#fc8c84"])

其他可以选的 option

加title，调大小，什么的，目前还没有优化，后续会精简一下

mqqplot(insumstats,
          chrom,
          pos,
          p,
          scaled=False,
          cut=0,
          cutfactor=10,
          cut_line_color="#ebebeb",
          windowsizekb=500,
          anno=None,
          sig_level=5e-8,
          sig_line_color="grey",
          suggestive_sig_level=5e-6,
          title =None,
          mtitle=None,
          qtitle=None,
          figsize =(15,5),
          fontsize = 10,
          colors = ["#000042", "#7878BA"],
          layout="qqm",
          verbose=True,
          repel_force=0.03,
          gc=True,
          save=None,
          saveargs={"dpi":300,"facecolor":"white"}        
          )

保存的话 save=“./yourpath/myplot.png” ,或者save=True就行

分别画Manhattan plot 与 QQ plot

当然也可以分开画 mplot

mymplot = gl.mplot(insumstats,"CHR","POS","PVALUE",cut=20,cutfactor=10,anno=True)

qqplot

参考：

https://github.com/Cloufield/gwaslab

GWAS Gallery: gwaslab

去哪找公开的GWAS数据 – Publicly Available GWAS Sumstats

目录

  1. 公共数据库
  2. 各大Biobank与Cohort
    • 欧美
    • 东亚
    • Global Biobank
  3. 单独的研究发表的数据
  4. 各类疾病研究组织的数据

本文将简要介绍可以简单入手的GWAS sumstats的一些来源，文中提及的来源都是公开可下载的，适合新入门的同学练手，做一些小规模的meta分析，或是post-gwas分析。

1.公共数据库：

目前收录最全的GWAS数据库，但只收录了已发表GWAS的数据，而且会有几个月到半年左右的延迟，使用时应该注意：

GWAS catalog: https://www.ebi.ac.uk/gwas/

OpenGWAS: https://gwas.mrcieu.ac.uk/

2.各大Biobank的公开数据：

规模较大的Biobank或Cohort会定期公开GWAS sumstats，这类数据有些未被收录在GWAS catalog中，一些gwas检验方法的作者也会使用其方法进行Biobank级别的GWAS分析，这类数据的表型覆盖较广：

2.1欧美：

Finngen 4 : https://r4.finngen.fi/about

Finngen 5 : https://r5.finngen.fi/about

Finngen 6 : https://r6.finngen.fi/about

UKB : https://pheweb.org/UKB-Neale/

UKB saige: https://pheweb.org/UKB-SAIGE/

UKB fastgwa-glmm: https://yanglab.westlake.edu.cn/resources/ukb_fastgwa/imp_binary/

UKB fastgwa: https://yanglab.westlake.edu.cn/resources/ukb_fastgwa/imp/

UKB TOPMed: https://pheweb.org/UKB-TOPMed/

UKB gene-based: https://genebass.org/

Pan-UKB : https://pan.ukbb.broadinstitute.org/

MGI 1 : https://pheweb.org/MGI-freeze1/

MGI 2 : https://pheweb.org/MGI-freeze2/

MGI BioUV: https://pheweb.org/MGI-BioVU/

FinMetSeq: https://pheweb.sph.umich.edu/FinMetSeq/

Generation Scotland: https://datashare.ed.ac.uk/handle/10283/844

2.2 东亚：

Biobank Japan:

JENGER: http://jenger.riken.jp/result

Pheweb: https://pheweb.jp/

ToMMo – JMorp：https://jmorp.megabank.tohoku.ac.jp/202109/gwas/

KoreanChip: https://www.koreanchip.org/downloads

KoGES Pheweb: https://koges.leelabsg.org/

2.3 全球范围Biobank的Meta分析：

近期Global Biobank项目也公开了一批全球范围biobank的常见复杂疾病meta分析

Global Biobank :http://results.globalbiobankmeta.org/

3.单独的研究发表的数据

直接在google上搜索研究论文，从Data availability里的url顺藤摸瓜找到数据，此类数据散落在各个学校，研究机构等等自家的网站上，没有好的办法，只有自己搜索。GWAS catalog 经常会出现收录不及时而漏掉很多最新数据。

例如：

Program in Complex Trait Genomics, IMB, The University of Queensland.

https://cnsgenomics.com/content/data

https://ctg.cncr.nl/software/summary_statistics

4.各类疾病研究组织的数据

这类数据通常为meta分析后的sumstats，例如：

DIAGRAM：http://www.diagram-consortium.org/downloads.html

Megastroke: https://www.megastroke.org/index.html

GIANT (Genetic Investigation of ANthropometric Traits)：https://portals.broadinstitute.org/collaboration/giant/index.php/Main_Page

GLGC (Global Lipids Genetics Consortium):  http://csg.sph.umich.edu/willer/public/glgc-lipids2021/

PGC (Psychiatric Genomics Consortium): https://www.med.unc.edu/pgc/download-results/

等等

一个人的总结难免会有疏漏，欢迎大家在评论里补充！

使用corrplot绘制遗传相关矩阵

统计遗传学研究中经常会需要通过GWAS的sumstats来计算遗传相关，并以一下这种简单易懂的相关矩阵形式展示，本文就以两篇高质量文章为例，来介绍遗传相关矩阵的绘图方法。

回顾：GWASLab：通过Bivariate LD Score regression估计遗传相关性 genetic correlation

上图为An atlas of genetic correlations across human diseases and traits（文章链接：https://www.nature.com/articles/ng.3406）中的遗传相关矩阵的图，可以看到图中蓝色方块表示正向相关，红色方块表示负向相关，其中相关显著的表型（经过多重检验调整后）之间还会被 * 标记。这幅图中，方块的大小与颜色均表示相关系数，但这幅图还有个特别之处是FDR<0.01的方块被填满。（注意，这里的方块大小依然是相关系数，但近来的文章中，方块大小通常会被用来表示p值的大小，后续会介绍）

接下来我们尝试复现这幅图：

源数据下载：https://static-content.springer.com/esm/art%3A10.1038%2Fng.3406/MediaObjects/41588_2015_BFng3406_MOESM37_ESM.csv

源数据格式如下：

$ head 41588_2015_BFng3406_MOESM37_ESM.csv
Trait1,Trait2,rg,se,z,p
ADHD,Age at Menarche,-0.153,0.08218,-1.858,0.063
ADHD,Age at Smoking,-0.036,0.2427,-0.147,0.883
ADHD,Alzheimer's,-0.055,0.2191,-0.249,0.803
ADHD,Anorexia,0.192,0.1162,1.649,0.099
ADHD,Autism Spectrum,-0.164,0.1438,-1.144,0.253
ADHD,BMI,0.287,0.08913,3.222,0.001
ADHD,BMI 2010,0.258,0.08606,2.993,0.003
ADHD,Bipolar,0.265,0.1539,1.722,0.085
ADHD,Birth Length,-0.055,0.1679,-0.329,0.742

使用R的官方corrplot来绘制，示例代码如下：

install.packages("corrplot")
library(corrplot)
#读取数据
ldsc = read.csv(file = '41588_2015_BFng3406_MOESM37_ESM.csv',header=TRUE)

#提取需要画的表型
to_plot_col<-c('Age at Menarche','Alzheimer\'s','Anorexia','Autism Spectrum','BMI','Bipolar','Birth Length','Birth Weight','Childhood Obesity','Coronary Artery Disease','Crohn\'s Disease','Depression','Ever/Never Smoked','Fasting Glucose','HDL','Height','Infant Head Circumference','LDL','Rheumatoid Arthritis','Schizophrenia','T2D','Triglycerides','Ulcerative Colitis','Years of Education')

#构建一个rg矩阵，和一个p值矩阵,并命名row和col
gcm_rg<-matrix(1, nrow = length(to_plot_col), ncol = length(to_plot_col))
gcm_p<-matrix(1, nrow = length(to_plot_col), ncol = length(to_plot_col))
rownames(gcm_rg) <- to_plot_col
colnames(gcm_rg) <- to_plot_col
rownames(gcm_p) <-to_plot_col
colnames(gcm_p) <- to_plot_col

#将数据填进矩阵
for (row in 1:nrow(ldsc)) {
    if(ldsc[row, "Trait1"]%in%to_plot_col && ldsc[row, "Trait2"]%in%to_plot_col){
    Trait1 <- ldsc[row, "Trait1"]
    Trait2  <- ldsc[row, "Trait2"]
    gcm_rg[Trait1,Trait2]<-ldsc[row, "rg"]
    gcm_p[Trait1,Trait2]<-p<-ldsc[row, "p"]
    gcm_rg[Trait2,Trait1]<-ldsc[row, "rg"]
    gcm_p[Trait2,Trait1]<-p<-ldsc[row, "p"]
    }
    }

#使用corrplot绘图：（方法选择square）
#sig.level = 0.05/300 为显著水平（这里是多重检验调整的）
#gcm_rg为相关系数矩阵
#gcm_p为p值矩阵
#order="hclust" 为通过分层聚类对矩阵进行排序
#其他选项均为细节调整 可以参考 https://cran.r-project.org/web/packages/corrplot/vignettes/corrplot-intro.html 

corrplot(gcm_rg, p.mat=gcm_p, method="square",order="hclust",sig = "pch",sig.level = 0.05/300 ,pch="*",pch.cex=2,
         tl.col="black",tl.srt=45,addgrid.col="grey90")

对比与原图，已经接近90%的相似度了，不同之处在于这幅图还有个特别之处是FDR<0.01的方块被填满。这需要对底层代码进行修改。

这里我们就略过此步骤，因为目前主流方法是，方块大小应该表示p值大小, 以提高遗传相关矩阵的信息含量，而不是途中混合的表示方式。方块大小表示p值大小的示例，如下图所示：

（文章链接：https://www.nature.com/articles/s41588-018-0047-6）

这张图中颜色表示相关系数，方块大小表示p值（fdr调整后）

这篇文章的作者提供了修改后的代码，可以通过github在R中安装修改后的corrplot：

github: https://github.com/mkanai/ldsc-corrplot-rg

install.packages("dplyr")
devtools::install_github("mkanai/corrplot")

安装后重新绘制：

#读取数据
ldsc = read.csv(file = '41588_2015_BFng3406_MOESM37_ESM.csv',header=TRUE)

#计算FDR调整后p值
ldsc$fdr<-p.adjust(ldsc$p, method ="fdr")

to_plot_col<-c('Age at Menarche','Alzheimer\'s','Anorexia','Autism Spectrum','BMI','Bipolar','Birth Length','Birth Weight','Childhood Obesity','Coronary Artery Disease','Crohn\'s Disease','Depression','Ever/Never Smoked','Fasting Glucose','HDL','Height','Infant Head Circumference','LDL','Rheumatoid Arthritis','Schizophrenia','T2D','Triglycerides','Ulcerative Colitis','Years of Education')

gcm_rg<-matrix(NA, nrow = length(to_plot_col), ncol = length(to_plot_col))
gcm_p<-matrix(NA, nrow = length(to_plot_col), ncol = length(to_plot_col))
rownames(gcm_rg) <- to_plot_col
colnames(gcm_rg) <- to_plot_col
rownames(gcm_p) <-to_plot_col
colnames(gcm_p) <- to_plot_col

#p值矩阵改为fdr矩阵
for (row in 1:nrow(ldsc)) {
    if(ldsc[row, "Trait1"]%in%to_plot_col && ldsc[row, "Trait2"]%in%to_plot_col){
    Trait1 <- ldsc[row, "Trait1"]
    Trait2  <- ldsc[row, "Trait2"]
    gcm_rg[Trait1,Trait2]<-ldsc[row, "rg"]
    gcm_p[Trait1,Trait2]<-ldsc[row, "fdr"]
    gcm_rg[Trait2,Trait1]<-ldsc[row, "rg"]
    gcm_p[Trait2,Trait1]<-ldsc[row, "fdr"]
    }
    }

#事先对矩阵进行排序（此修改的版本直接使用order="hclust"时有bug）
gcm_rg.hclust<-corrMatOrder(gcm_rg,order ="hclust")
gcm_rg_hclust<-gcm_rg[gcm_rg.hclust,gcm_rg.hclust]
gcm_p_hclust<-gcm_p[gcm_rg.hclust,gcm_rg.hclust]

options(repr.plot.width=15, repr.plot.height=15)
#使用修改后的corrplot绘图：（注意！！方法选择 psquare）
corrplot(gcm_rg_hclust ,p.mat=gcm_p_hclust, diag=FALSE,method="psquare",sig="pch",insig="label_sig",sig.level = 0.01 ,pch.cex=2,tl.col="black",tl.srt=45,addgrid.col="grey90")

修改后的图图例更为统一，对于p值大小的表现更为清楚。

对于图中的排序方法，字体大小，旋转，颜色, 色调，colorbar等等细节可以参考 https://cran.r-project.org/web/packages/corrplot/vignettes/corrplot-intro.html 进行调整。

参考：

https://www.nature.com/articles/ng.3406#MOESM37

https://www.rdocumentation.org/packages/corrplot/versions/0.92/topics/corrplot

https://cran.r-project.org/web/packages/corrplot/vignettes/corrplot-intro.html

https://www.nature.com/articles/s41