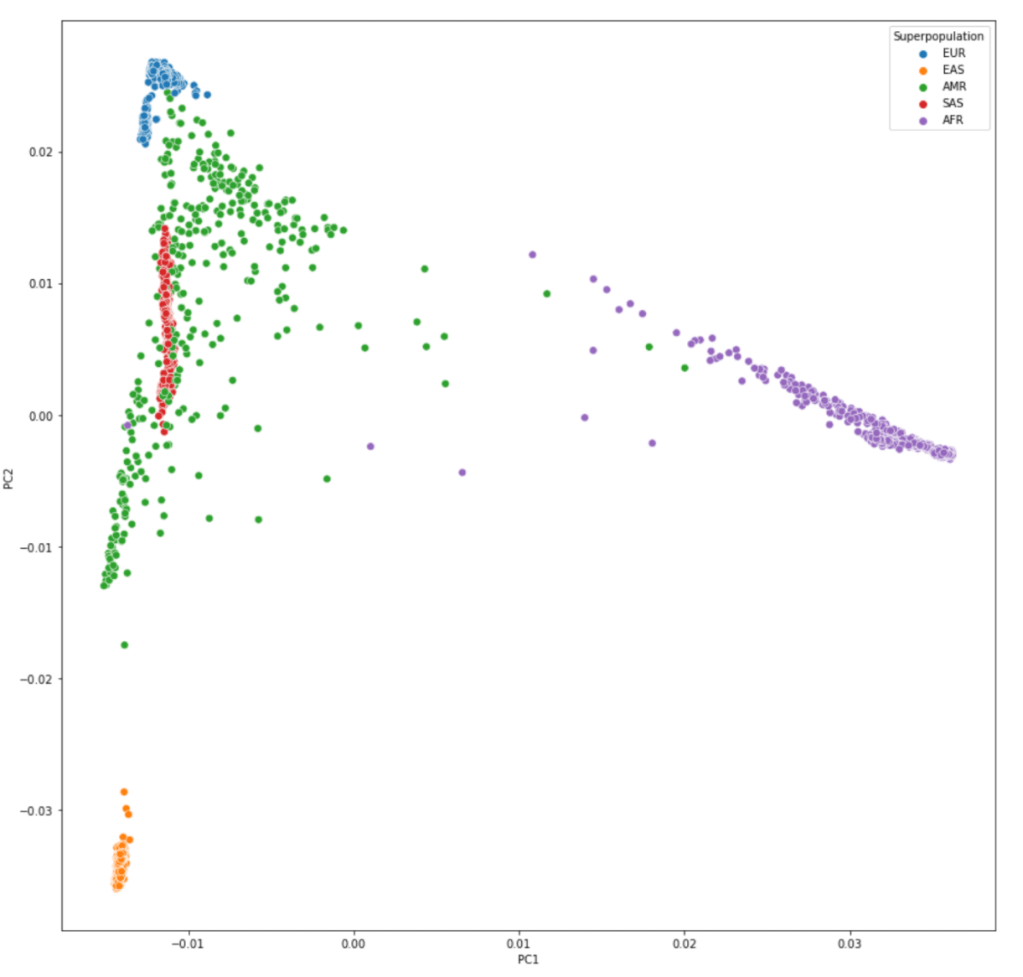
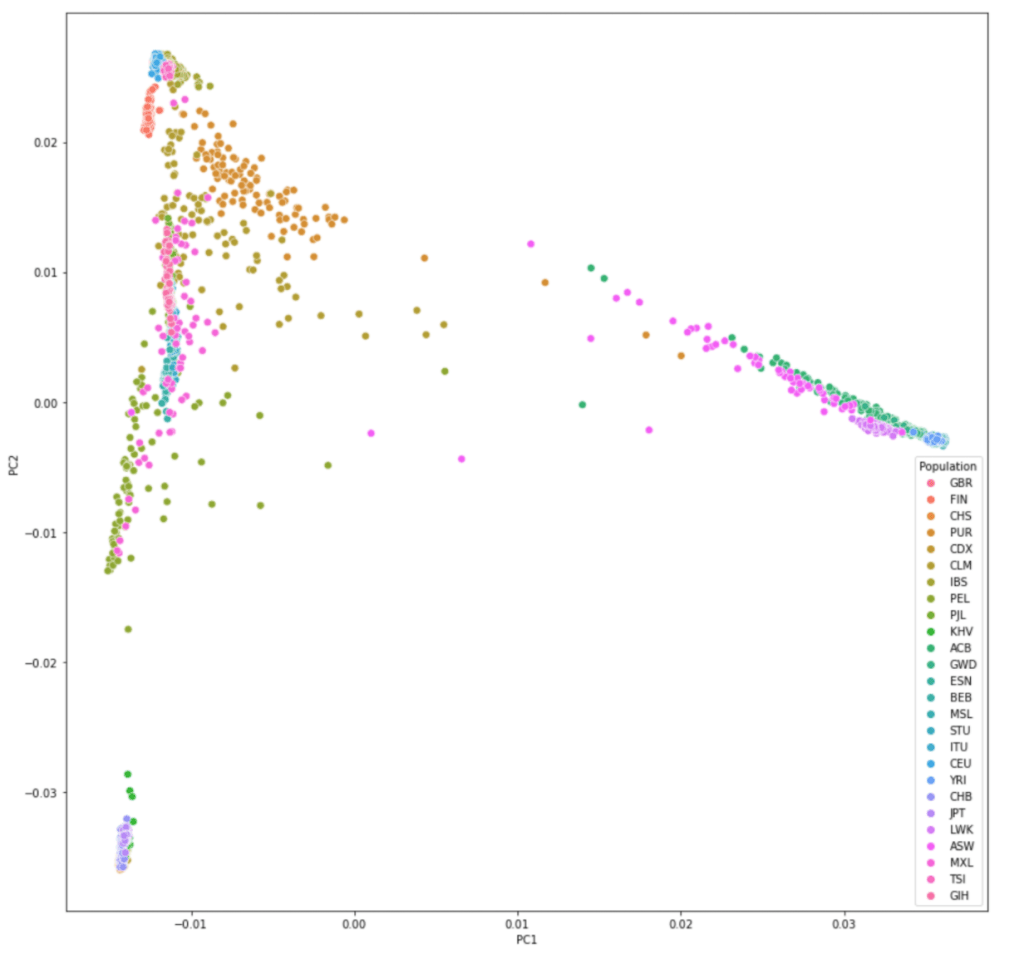
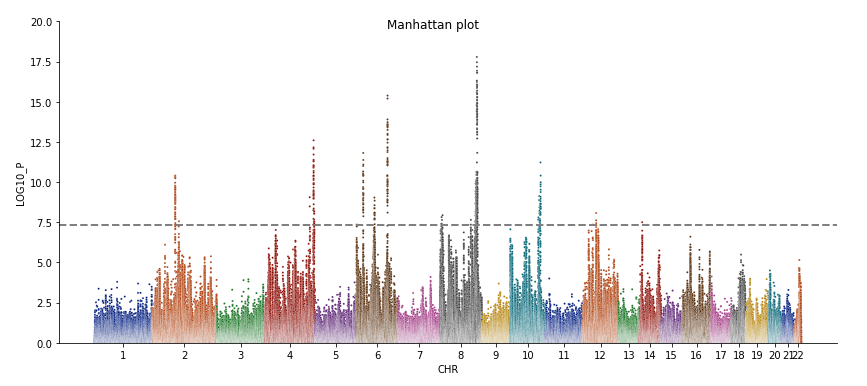
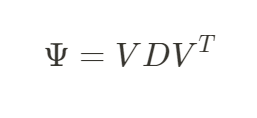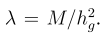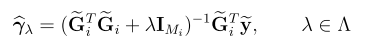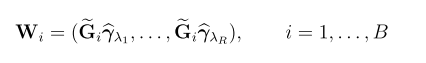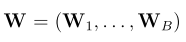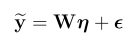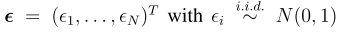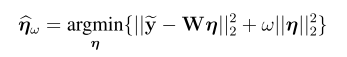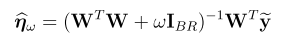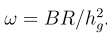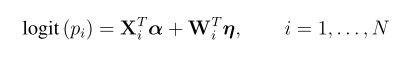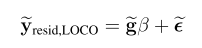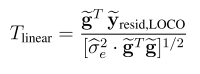一，简介
COSI2是一款基于溯祖理论(Coalescent theory)的模拟软件, 可以用来模拟群体的单倍型。
url：https://github.com/broadinstitute/cosi2
从github上clone到本地后，解压并编译
tar xvfz cosi-2.0.tar.gz
cd cosi-2.0
./configure
make
二，使用方法
基本语法
coalescent -p paramfile -m
-p 是指定参数文件；-m 是指定输出文件格式为Richard Hudson’s ms simulator的输出格式， 可以参考http://home.uchicago.edu/rhudson1/source/mksamples.html
参数文件中可以通过关键字来定义群体结构等各类模拟参数。
1.1. 指定模拟的范围长度，单位是 basepairs
length <length in bp>
1.2. 突变率
mutation_rate <mutation rate per bp per generatio>
1.3.重组率
recomb_file <file-name>
需要指定额外的 genetic map 文件，这个文件包含两列，有空格分隔。第一列给出基于碱基对的位置，第二列给出到下一位点的交叉重组率（每代）。第一列需要为严格的升序。 只有一行的文件则代表恒定的重组率。
例如：
1 9.92772e-09
156 1.00420e-08
373 1.01177e-08
923 9.77556e-09
1666 9.29830e-09
2704 9.19754e-09
附带的 recosim (在文末介绍) 程序也可以基于给定的重组热点的分布来随机生成一个genetic map。
2 群体
任何出现在模拟中的群体都需要被明确指定
pop_define <pop id> <label>
pop_size <pop id> <size>
sample_size <pop id> <n samples>
pop id 为整数值，在之后描述demographic events时会用到。 label 则是方便我们阅读用的标签。pop_size 是指群体中二倍体的数量。sample则指单倍体样本的数量。
例如
pop_define 1 European
pop_size 1 10000
sample_size 1 50
指定了ID为1的 ‘‘European’’群体，大小为10000，抽取的单倍体样本为50
3. demographic history 群体变迁史
#population size
pop_event change_size <label> <pop id> <T> <size for time > T>
#exponential expansion
pop_event exp_change_size <label> <pop id> <Tend> <Tstart> <final size> <start size>
pop_event exp_change_size "expansion" 1 50 500 10000 1000
# bottleneck event
pop_event bottleneck <label> <pop id> <T> <inbreeding coefficient>
#migration rate
pop_event migration_rate <label> <source pop id> <target pop id> <T> <probability of migration/chrom/gen>
#population split
pop_event split <label> <source pop id> <new pop id> <T>
#admixture
pop_event admix <label> <admixed pop id> <source pop id> <T> <fraction of admixed chroms from source>
#sweep
pop_event sweep <pop> <Tend> <selection coefficient> <position of causal allele (0.0-1.0)> <freq at Tend>
输出格式：
-m 结果格式为 Richard Hudson’s ms simulator 的格式，直接打印在标准输出里。
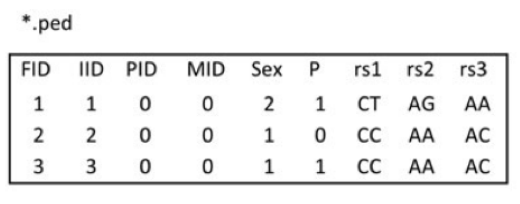
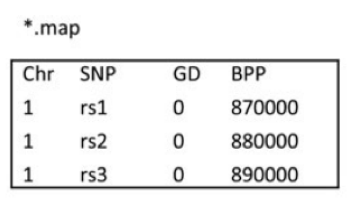
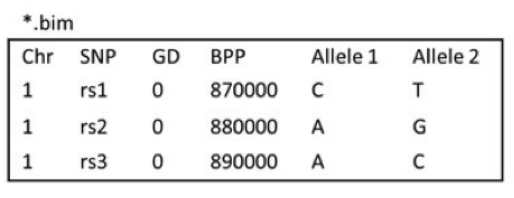
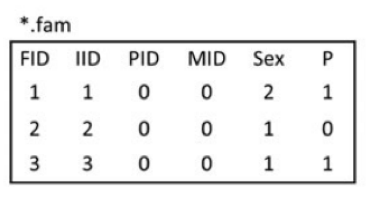
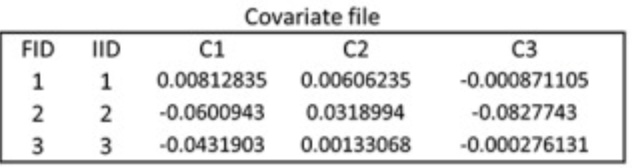
-o basename 生成cosi的格式，对于每个群体，分别生成basename.pos-<pop id> 与 basename.hap-<pop id> 文件。basename.hap-<pop id>包含了单倍体型， basename.pos-<pop id> 则是变异的位置。在 basename.hap-<pop id> 中，2指代祖先的allele，1则是衍生的allele。
例：
# basename.hap-<pop id>
0 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 ...
# basename.pos-<pop id>
SNP CHROM CHROM_POS ALLELE1 FREQ1 ALLELE2 FREQ2
1 1 85.409249 1 0.000000 2 1.00000
...
三，使用 recosim 生成recombination maps
用法： recosimulate <parameter file name> <region size (bp)>
用于生成 recombination maps 的参数文件如下：（所有参数都是可选的）
outfile <output file name> [default="model.out"]
model <0,1> [default=0]
model 0: uniform recombination, constant or drawn from distribution.
model 1: model 0 + gamma-distributed hotspots.
baserate <mean recomb (cM/Mb)> [default=1.0]
distribution <recomb distr. file name> [default=none (const value)]
space <mean hotspot spacing (bp)> [default=9000]
distance_shape <gamma function shape param> [default=1.0]
intensity_shape <gamma function shape param> [default=0.3]
local_shape <gamma function shape param, local variation> [default=0.3]
local_size <size of region of local variation (bp) (e.g. 100000)> [default=50000000]
bkgd <fraction in flat bkgd> [default=0.1]
random_seed <integer seed> (0=>picked by program based on time and PID) [default=0]
如果使用 model 0 ，那么重组率对于模拟的区域来说是恒定的，可以通过 baserate 来直接指定，也可以通过 distribution 来从指定分布文件中随机生成。
分布文件格式如下：
bin_start bin_end cumulative_fraction
Where bin_start and bin_end specify a range of recombination rates (in cM/Mb) and the cumulative fraction is the probability that the recombination rate lies within this or earlier bins. Entries should be in order of increasing rate;
例：examples/bestfit/autosomes_deCODE.distr
0.0 0.2 0.05052
0.2 0.4 0.14890
0.4 0.6 0.27919
0.6 0.8 0.40295
0.8 1.0 0.50370
1.0 1.2 0.59713
1.2 1.4 0.66145
1.4 1.6 0.71358
1.6 1.8 0.77198
1.8 2.0 0.80874
2.0 2.2 0.84086
2.2 2.4 0.86372
2.4 2.6 0.88945
2.6 2.8 0.91396
...
如果使用 model 1 ，重组率则是变化的。
the recombination rate varies across the region; the variation can be on both local and fine scales. With this model, the baserate or distribution parameters are still valid, but they now set the expected value of the recombination rate in the entire region, the value around which local rates vary. A fraction of the mean rate can be kept constant across the region, using the bkgd parameter. The remainder of the recombination rate varies locally in windows across the region, with the size of the window controlled by the parameter local_size; that is, if local_size is set to 100 kb, a new value is chosen every 100 kb. The value is chosen from a gamma distribution (with shape parameter set by local_shape), with a mean value determined by the regional rate (and the background fraction). Within each window, recombination is clustered into point-like hotspots of recombination. These have a gamma-distributed intensity with shape parameter intensity_shape (and mean determined by the local rate), and a gamma-distributed spacing with shape parameter distance_shape and mean set by parameter space.
With model=1 and a small value for intensity_shape, there is a small but extended tail at very high recombination rates; when simulating long sequences, this can make the coalescent simulator take orders of magnitude longer on a small fraction of runs. I have therefore found it useful to truncate the tail within recosim. (There is a commented-out line for doing so in the code.)
A final option is random_seed, which permits the user to specify a seed for the random number generator; this is useful for debugging or recreating a previous run. If a seed of zero is supplied, or the keyword is not found, a random seed will be generated from the time and process id of the job. In any case, the random seed used is always output to stdout during execution.
附录：
cosi2命令行选项
Specifying the model:
-p [ --paramfile ] arg parameter file
-R [ --recombfile ] arg genetic map file (if specified, overrides the
one in paramfile)
-n [ --nsims ] arg (=1) number of simulations to output
-r [ --seed ] arg (=0) random seed (0 to use current time)
-J [ --trajfile ] arg file from which to read sweep trajectory. It has two columns: first column gives the generation, second gives the fraction of chromosomes in the sweep population carrying the derived (advantageous) allele.
-u [ --max-coal-dist ] arg (=1) for Markovian approximation mode, the level
of approximation: the maximum distance
between node hulls for coalescence to be
allowed. Distance is specified as a fraction
of the total length of the simulated region,
in the range [0.0-1.0]; 1.0 (default) means
no approximation.
Specifying the output format:
-o [ --outfilebase ] arg base name for output files in cosi format
-m [ --outms ] write output to stdout in ms format
Specifying output details:
-P [ --output-precision ] arg number of decimal places used for floats in the outputs
-M [ --write-mut-ages ] output mutation ages
-L [ --write-recomb-locs ] output recombination locations
Misc options:
-h [ --help ] produce help message
-V [ --version ] print version info and compile-time options
-v [ --verbose ] verbose output
-g [ --show-progress ] [=arg(=10)] print a progress message every N
参考：
![E[\chi^2|l_j] = {{Nh^2l_j}\over{M}} + Na + 1](https://s0.wp.com/latex.php?latex=E%5B%5Cchi%5E2%7Cl_j%5D+%3D+%7B%7BNh%5E2l_j%7D%5Cover%7BM%7D%7D+%2B+Na+%2B+1&bg=ffffff&fg=333333&s=3&c=20201002)
GWASLab - GWAS实验室 