GWAS 全基因组关联分析 – 第 6 页 – GWASLab

血缘系数/ 近交系数/ 亲缘系数 coefficient of kinship / inbreeding / relationship

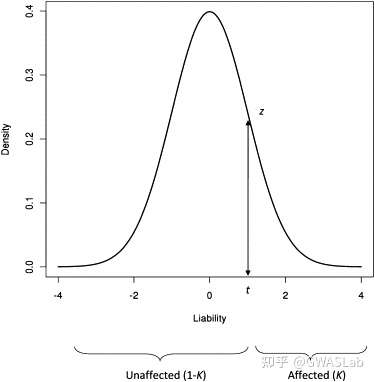
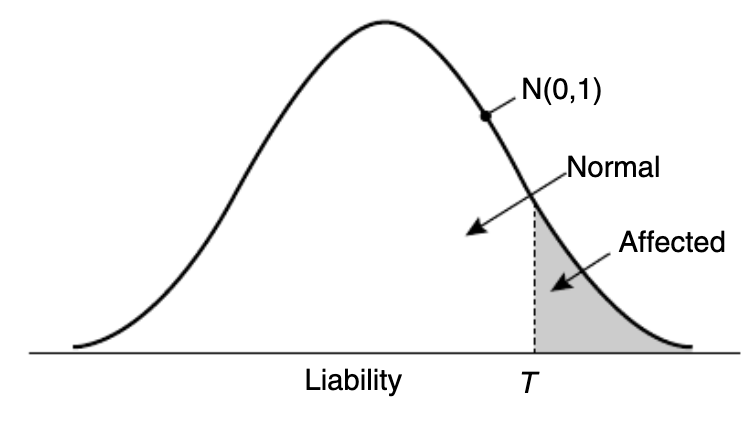
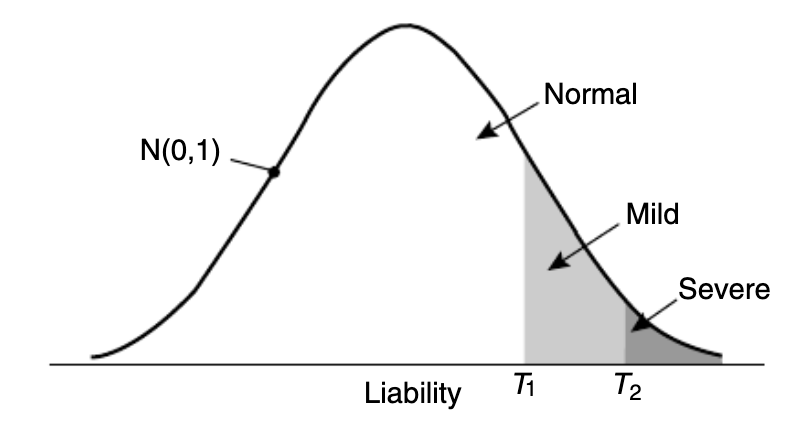
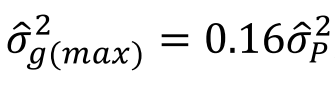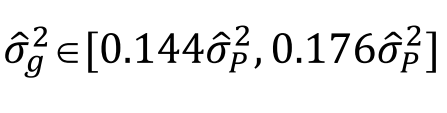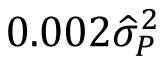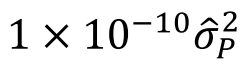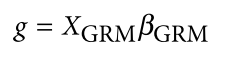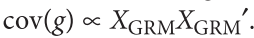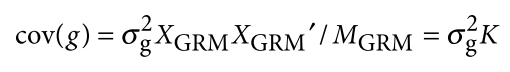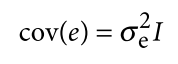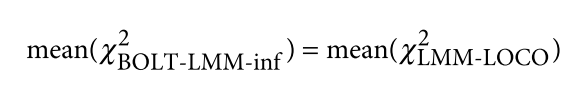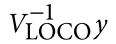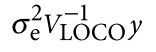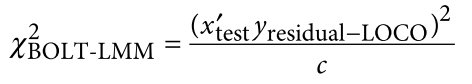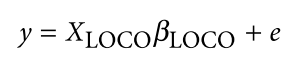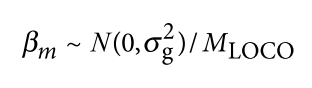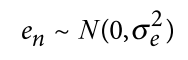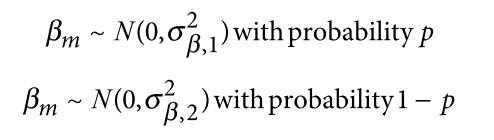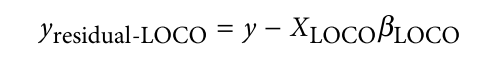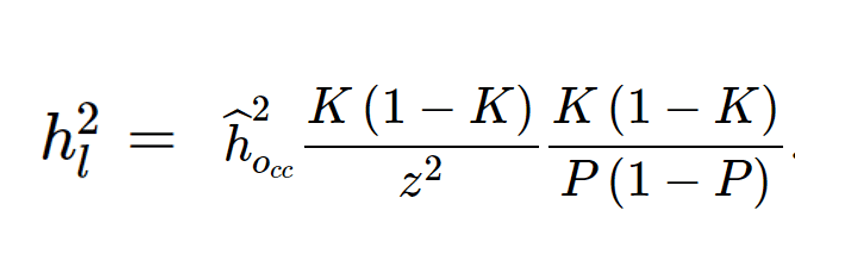遗传学中关于亲缘关系的常见的几个系数辨析：

血缘系数 coefficient of kinship / kinship coefficient，有些地方称为近亲系数，有时也称共祖系数 coefficient of coancestry，（目前缺少权威的中文翻译），是对个体间血缘关系的直接衡量，定义为从两个个体随机抽取一个同源等位基因，所抽取的两个等位基因是血缘同源（IBD）的概率（即这两个等位基因相同，且来自同一个祖先）。

常用的用来衡量亲缘关系的，且容易混淆的系数还有如下两个，近交系数与血缘系数。

近交系数 coefficient of inbreeding ，由怀特（ Wright, Sewall ）最早定义，是指 一个个体的某个基因座上的两个等位基因为血缘同源（IBD）的概率，衡量的是这个个体父母间亲缘程度的大小，反映的是近亲交配的程度。有时也称为固定系数 fixation index ，通常用 F 表示。

亲缘系数 coefficient of relationship / coefficient of relatedness ，该系数也由怀特定义，衍生自他对近交系数的定义，是指有共同祖先的两个个体间，基因型一致的概率，通常用 r 来表示。数值上是 血缘系数 的两倍。

对于常见亲缘关系这三个系数的理论值如下图所示：

与个体的关系	血缘系数	近交系数 F	亲缘系数 r
自己，同卵双胞胎	1/2	1/2	1
亲兄弟姐妹	1/4	1/4	1/2
母父，儿女*	1/4	1/4	1/2
祖父母，孙子孙女	1/8	1/8	1/4
舅舅，舅妈，侄女，侄子	1/8	1/8	1/4
表兄弟	1/16	1/16	1/8
同父异母或同母异父的兄弟姐妹	1/8	1/8	1/4

*注意，虽然近交系数与血缘系数值相等，当他们的概念并不相同。

血缘系数是指两个个体间的血缘关系，如（母父，儿女）这一项，血缘系数为1/4的意思是从一个个体与其亲生父母或孩子个随机抽取一个同源等位基因，这两个等位基因相同，且来自同一个祖先的概率是1/4.

而近交系数在这里的值为虽然也为1/4，但其表达的意思是如果这个个体与其亲生父母或孩子近交后，子代的某个基因座上的两个等位基因为血缘同源的概率为1/4.

参考：

Wright, Sewall (1922). “Coefficients of inbreeding and relationship”. American Naturalist. 56 (645): 330–338. doi:10.1086/279872.

SNP的LD剪枝与聚集 LD pruning & clumping

GWAS相关的研究中，很多时候我们需要从总的SNP数据中，基于SNP两两之间的LD，来抽取出一个不含互相关联SNP的子集，目前主要的两种方法分别是 LD pruning 与 clumping。

例如，

在进行主成分分析（PCA）时，我们需要事先对SNP进行LD pruning 以去除互相关联（处于LD）的SNP，以防止高LD区域过高的方差对结果的影响。

在计算风险分数PRS时，我们需要从显著的loci中选取具有代表性的SNP来计算分线分数，这时就需要进行clumping，基于LD的r2，以及GWAS所得到的p值，来筛选出这个LD区域中的代表SNP（重要性最高），这样我们可以获得更准确的风险分数。

LD pruning 与 clumping 方法的异同如下所示：

	根据	保留	主要用途
Pruning	LD的R2	处于LD的一对SNP中MAF最高的	PCA
Clumping	LD的R2 与 SNP的P值	处于 LD的一对SNP中P值最显著的	PRS

Pruning 与 clumping 的主要区别

具体算法上，可以简单理解为：

Pruning：选取第一个SNP，然后计算这个SNP与窗口区间里第二个，第三个，等等的r2，当检测到高的相关性时，就会从这一对SNP中去除MAF较低的那个，保留 MAF 高的，也就是说这个过程中可能会去除掉我们选的第一个SNP。完成后下一步就是选取下一个SNP，重复这个过程。

Clumping：首先会依据从GWAS得到的p值对SNP的重要性进行排序，然后选取排序后的第一个SNP，计算这个SNP与窗口区间里其他SNP的r2，当检测到高的相关性时，就会从这一对SNP中去除重要性低的那个，这个过程中我们选的第一个SNP一定会得到保留。完成后下一步就是选取 p值排序后的下一个 SNP，重复这个过程。

PLINK中提供了 Pruning 和 Clumping 的功能：

Pruning：

我们主要是用–indep-pairwise选项，也就是根据SNP两两之间的LD来pruning。

--indep-pairwise  <window size>['kb']  <step size (variant ct)>  <r^2 threshold>

例 --indep-pairwise 500 50 0.2
这三个参数代表的意思分别是： 窗口大小，每一步移动窗口的距离，以及判定关联的r2阈值

plink -bfile input --indep-pairwise 500 50 0.2 --out input_pruned

输出两个文件
input_pruned.prune.in    #pruning后保留的互不相关的SNP
input_pruned.prune.out  #去除掉的SNP

Clumping:

PLINK提供了多种参数选项，具体可以参考：https://www.cog-genomics.org/plink/1.9/postproc

参考：

https://www.cog-genomics.org/plink/1.9/postproc

https://www.cog-genomics.org/plink/1.9/ld

https://www.biostars.org/p/343818/

LiftOver 基因组坐标变换

本文内容：

liftover 简介与网页版工具
liftover 命令行工具使用方法
基于0的坐标系统与基于1的坐标系统之间的转换

人类参考基因组不同版本之间基因坐标不同，进行研究时我们需要统一基因组坐标系，从一个版本的坐标系向另一个坐标系转换的过程就称之为liftover，UCSC，ensembl等为我们提供了便捷的工具，本文以 UCSC 的liftOver工具为例：

首先UCSC liftOver工具提供了即开即用的网页版：http://genome.ucsc.edu/cgi-bin/hgLiftOver

选择目标物种，新旧基因组版本，粘贴或上传原文件就可以开始liftover。

但更多时候我们需要使用命令行的工具，以下，本文主要介绍liftOver的命令行版本，下载地址：http://hgdownload.soe.ucsc.edu/downloads.html

liftover的url: http://hgdownload.soe.ucsc.edu/admin/exe/linux.x86_64/liftOver

下载完成后添加到环境路径中，并通过chmod +x 添加执行权限，然后在命令行中输入liftOver验证是否安装成功：（如果成功会有如下界面）

liftOver主要语法如下：

liftOver <输入文件> <chain文件> <输出文件> <unmapped文件>

input/output 可以使用bed格式文件，chain file 则需要我们根据转化前后的数据库在ucsc上下载，无法转换的条目则输出到unmapped文件里。

这里以hg19->hg38为例，进行liftover，首先下载hg19tohg38的chain文件，下载地址为： http://hgdownload.soe.ucsc.edu/downloads.html#source_downloads

点击hg19的liftover files后下载对应文件：

下载完成后不需解压即可开始使用：

liftOver input.bed hg19ToHg38.over.chain output.bed unmapped.txt

input.bed

就转换成了： output.bed

在进行LiftOver时，有一点需要我们注意，那就是文件中变异位点起始的编号，是基于0还是基于1的。

因为 UCSC 使用基于0的坐标系统，而 Ensembl 等使用基于1的坐标系统，不同工具切换时应该注意这一不同。

除此以外，一些文件格式是基于1的（GFF, SAM , VCF），而另一些是基于0的（BED，BAM），不同文件间转换时也需要注意。

基于0和基于1的坐标系统示可以理解为：

基于1的坐标系：对核苷酸直接编号。

基于0的坐标系：对两个核苷酸之间的间隙编号。

在表示单核苷酸或多个核苷酸变异时，

基于1的坐标系：直接使用变异位点的编号。

基于0的坐标系：变异两边的位置作为起止。

表示insert或deletion时，

基于1的坐标系：Deletion直接使用相应位点编号，insertion则是插入位置两边的核苷酸编号。

基于0的坐标系： Deletion 是插入位置两边的间隙编号表示， Insertions 则直接由插入间隙的编号表示。

基于1的坐标系与基于0的坐标系互相转换时，伪代码如下：

从基于0的坐标系向基于1的坐标系转换：

if (type=SNV){start=start+1; end=end;}
if (type=DEL){start=start+1; end=end;}
if (type=INS){start=start; end=end+1;}

从基于1的坐标系向基于0的坐标系转换：

if (type=SNV){start=start-1; end=end;}
if (type=DEL){start=start-1; end=end;}
if (type=INS){start=start; end=end-1;}

参考：

https://www.biostars.org/p/84686/

https://genome.ucsc.edu/cgi-bin/hgLiftOver

http://hgdownload.soe.ucsc.edu/downloads.html#liftover

群体分化系数 Fst Fixation index

群体分化系数（Fst，Fixation index）是用来衡量两群体间遗传距离的指标，多基于群体的SNP数据来估计。

目前主流的定义有两种，分别基于等位基因频率，或是血缘同源（IBD）。

如果 $\bar{p}$ 是某个等位基因在整个群体里的频率, $\sigma _{S}^{2}$ 是等位基因在不同亚群体之间的被群体大小加权后的频率的方差（组间方差）， $\sigma _{T}^{2}$ 是整个群体的等位基因频率的方差。那么Fst可以被定义为：

$F_{{ST}}={\frac {\sigma _{S}^{2}}{\sigma _{T}^{2}}}={\frac {\sigma _{S}^{2}}{{\bar {p}}(1-{\bar {p}})}}$

Wright的定义表示Fst衡量了群体结构可以解释的遗传变异的量。换句话说，衡量的是不属于亚群内多样性的多样性（组间多样性）所占总体多样性的比值，其中多样性通过两个随机抽取的等位基因是不同的概率估计，也就是2p（1-p）。

如果在第i个群体的等位基因频率为pi，相对大小为ci，那么Fst可以表示为：

$F_{{ST}}={\frac {{\bar {p}}(1-{\bar {p}})-\sum c_{i}p_{i}(1-p_{i})}{{\bar {p}}(1-{\bar {p}})}}={\frac {{\bar {p}}(1-{\bar {p}})-\overline {p(1-p)}}{{\bar {p}}(1-{\bar {p}})}}$

或者我们可以将Fst表示为：

$F_{{ST}}={\frac {f_{0}-{\bar {f}}}{1-{\bar {f}}}}$

其中f0是给定两个来自同一亚群体的个体，这两个个体血缘同源（IBD）的概率，

${\bar {f}}$ 则是给定两个来自总体的个体，这两个个体血缘同源（IBD）的概率。

通过这样的定义，Fst也可以被理解为相比于整体，两个个体在亚群体中相似性的高低。

实践中，Fst定义中所需要的数据一般都很难直接测量，所以通常我们都采用估算的方法。对于DNA序列数据，一个最简单的估计值就是：

$F_{{ST}}={\frac {\pi _{{\text{Between}}}-\pi _{{\text{Within}}}}{\pi _{{\text{Between}}}}}$

其中 $\pi _{{\text{Between}}}$ 与 $\pi _{{\text{Within}}}$ 分别代表两个不同亚群或相同亚群的个体之间，成对等位基因之间不同的平均值（average number of pairwise differences）。

参考：

https://en.wikipedia.org/wiki/Fixation_index

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1205159/

gnomAD 数据库: The Genome Aggregation Database

一，数据库简介

gnomAD是目前收录范围最广的基因组变异数据库之一，包含了全世界各人种的变异数据。gnomAD 与有较长历史的dbSNP的主要不同点在于，dbSNP包括了通过各种各样研究方法不同的项目而发现的基因组变异，dbSNP对这些变异加以整理，给予ID，但 gnomAD 为了能够正确的算出等位的频率，对所纳入样本的二代测序数据进行了统一标准的解析，这是 gnomAD 的一大特点。另外，对于50bp以上的基因组结构变异， gnomAD 也有着较高质量的数据。

目前版本 gnomAD v3.1 所包含数据汇总如下：

Population	Description	Genomes
afr	African/African-American	20,744
ami	Amish	456
amr	Latino/Admixed American	7,647
asj	Ashkenazi Jewish	1,736
eas	East Asian	2,604
fin	Finnish	5,316
nfe	Non-Finnish European	34,029
mid	Middle Eastern	158
sas	South Asian	2,419
oth	Other (population not assigned)	1,047

gnomAD 的前身是ExAC (Exome Aggregation Consortium), ExAC 只包含外显子组数据，目前已经被 gnomAD 取代。 gnomAD 的主要资助者是 the Broad Institute。

gnomAD的主页：

二，搜索基因

以ALDH1A1为例，页面最上端显示了基因的基本信息，右边Dataset处可以选择不同的subset（例如 non-cancer, non-neuro等等），Constraint处显示了synonymous，missense 以及 pLoF（基因丧失功能的可能性）的统计值，接下来的图标显示了每个部分的测序深度。

点击 show transcript 或者 show tissue也可以看到不同的transcript 或是在不同组织中的表达。

接下来是ClinVAr中收录的变异位点，与gnomAD中收录的位点的位置信息。

最后则是对变异位点的功能注释：

三，搜索变异

以ALDH2上的rs671为例，

我们可以找到该变异在数据库中的基本信息，包括频数，频率等，之后紧跟着对该变异的注释：

之后是该变异在ClinVar数据库中的信息：

然后是该变异在各群体中的详细的频率信息，以及年龄分布信息。

gnomAD还提供了该变异的质量信息。

最后还提供了便捷的浏览器，可以直观地在基因组中浏览该变异。

gnomAD内所有的信息均提供免费的下载服务，如果有需要也可以按需下载。

参考：

https://gnomad.broadinstitute.org/about

基于LMM的一种快速的关联检验方法 fastGWA

TL；DR

一句话总结：fastGWA是基于LMM的检验方法，该方法应用了一种快速的估算方法（fastGWA-REML，也就是网格搜索），可以避免计算协方差矩阵V的逆，从而大幅提升计算速度。

背景：

目前基于线性混合模型（LMM）的检验方法已经被广泛应用于GWAS研究中，因为LMM可以矫正群体分层以及亲缘关系。基本的原理就是以从所有SNP估计而来的样本结构为条件，检验变异与表型的关联。详见 LMM模型。

然而该模型的运算时间过长，目前的方法时间复杂度约为 O(mn2）到 O(m2n)之间，其中m是变异的数量，n是样本大小。

基于此背景，fastGWA旨在运用一种及其节省运算资源的算法，来进行基于LMM的GWAS分析，该方法内置在GCTA软件中。

fastGWA的LMM模型：

一般情况下LMM模型需要通过REML来估计参数，fastGWAS采用了以下的算法来简化计算，提升速度。

fastGWA-REML 算法：grid search（加速的重点）：

计算 log-likelihood scores 时，将g的方差可能的取值范围，等间距取100个值，

所以每一步的间隔就是

注意，这里可能的取值上限取了大于表型方差的值，原因是要尽可能的包含各种情况，包括当真实的遗传力较大，且环境因素影响也十分显著时， g的方差估计值可能大于表型方差。

接下来，要细化搜索窗口，在前面100个取值点中，log-likelihood scores 取最大值的点周围，20%的范围内，再细分16步：

也就是说如果第一步

那么就要在下面的范围里，再细分出16个取值点，

每步的大小如下，

接下来不断重复这个步骤，直到两次细分后找的最大值只差小于：

这样我们就可以相对快速而精准的估计出随机效应方差的大小。

有了估计的协方差矩阵，我们就能利用一般化的最小二乘法估计效应量beta，算式如下：

参考：

Jiang L, Zheng Z, Qi T, et al. A resource-efficient tool for mixed model association analysis of large-scale data[J]. Nature genetics, 2019, 51(12): 1749-1755.

https://cnsgenomics.com/software/gcta/#Overview

解释复杂疾病的四种主流模型 CDCV/RAME/infinitesimal/Broad-sense-heritability

一，常见疾病-常见变异假说 Common Disease Common Variant Hypothesis

该模型主要是指常见病的易感性主要由中等数量的常见变异引起。此假设有两个关键点，一是常见变异的效应相比于稀有变异应该较小，二是常见变异只有较小效应而常见病又有遗传力的话，那么一定有多个常见变异共同影响疾病易感性。早期的GWAS都是基于这一简单地假设。但这一假设有明显的不足，CDCV无法解释消失的遗传力的问题（ missing heritability ），即基于CDCV的GWAS所发现的常见变异只能解释很小一部分推测的遗传力。所以其他模型也开始得到重视以解决这一问题。

二，主要效应的稀有变异模型 The rare alleles of major effect (RAME) model

RAME 模型主要是指常见病病因其实异质性非常高，也就是说，少量MAF<0.01的稀有变异可以促进疾病的发展。主要效应的原位变异可以解释个位数百分比的遗传力。该模型主要聚焦于由于单倍剂量不足或是功能获得性突变而引起的显性效应，这类效应能使得风险上升两倍或者更多。

三，无穷小模型 The infinitesimal model

近年来GWAS研究中无穷小模型逐渐流行。该模型认为复杂疾病的遗传变异是由于大量的，效应很弱（相对风险低于1.2）的变异引起。该模型解释了丢失的遗传力其实大部分是被隐藏了，由于大量对疾病有较弱效应的变异无法在检验中达到预设的显著阈值。目前很多GWAS关联检验方法都基于这一模型。

四，广义遗传力模型：非加性 GxG 与 GxE 相互作用，以及表观遗传效应

Broad sense heritability model: non-additive G×G and G×E interactions and epigenetic effects

广义遗传力模型认为常见变异的效应与稀有变异的效应不足以解释丢失的遗传力。该模型的主要支持依据就是目前在模式生物数量遗传研究中发现的基因型-基因型相互作用（G×G interactions; 也叫上位效应epistasis），以及基因型-环境相互作用（G×E interactions）。除此以外还包括研究越来越多的表观遗传效应，最为显著的就是亲源效应的遗传贡献，与DNA甲基化的继承。

X轴是SNP在染色体上的位置，Y轴是单个SNP所解释的疾病易感性方差的百分数（注意：一般曼哈顿图中y轴是-log10（P））。1，在CDCV模型中，少量的中等效应的loci会产生很强的信号。2，在RAME模型中，少数的稀有变异的因果效应在个别个体中有较强的效应，但不足以解释大部分方差。3，无穷小模型有少数显著的loci，若干在LD区块中的SNP也会显著。4，如果关联只出现在某种环境中（绿色与橙色的信号），那么在一个同时有两种环境混合的群体中，整体效应就会减弱（如箭头所示），只有很少的关联能够被检测，降低了所能解释的方差。

参考：

https://www.nature.com/articles/nrg3118

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5635617/

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2914559/

基于高斯混合模型的关联检验 Bolt-LMM – GWAS方法

Key words:　LMM，高斯混合模型，贝叶斯，无穷小模型，长尾分布

TL；DR

Bolt-LMM对SNP的效应拟合高斯混合模型，该算法使用一种快速的方差近似方法，计算近似的表型残差，并通过回顾性的分数检验统计量检验残差与待检验SNP的关联，这样就构建了表型预测的贝叶斯模型与频率学派关联检验的桥梁。同时，基于LD分数回归，还会对统计量进行调整。

背景：

在bolt-lmm论文发表时已出现的LMM方法有以下的不足：

需要大量的计算资源，时间复杂度高。
现有模型由于对遗传结构非最优化（suboptimal modeling assumptions regarding the genetic architectures）的假设，会导致power降低。当前标准的线性混合模型是基于无穷小模型（infinitesimal model），该模型假设所有的变异都是效应量很小的因果变异，各效应量相互独立，服从高斯分布，但实际情况中，对于复杂表型，因果loci的数量大约为1000个左右。

为了解决以上问题，Bolt-LMM采取了贝叶斯的观点修改了混合模型，新模型中SNP效应量服从非高斯的先验分布，以更好地反映效应量大小不同的loci的遗传效应。

方法详解：

BOLT-LMM算法包含四个步骤，每一步都需要若干次时间复杂度为O(MN)的迭代。 (1a) 估计方差系数； (1b) 计算无穷小混合模型下的关联统计量（Bolt-LMM-inf） (2a) 估计高斯混合模型的系数 (2b) 计算高斯混合模型下的关联统计量（Bolt-LMM）
简要推导：

标准的线性混合模型如下所示：

Y是表型，x是待检验的SNP，g是遗传效应，e是环境因素在无穷小模型下，遗传效应g可以表示为：

其中XGRM是一个NxM的矩阵，每一列都是某个SNP标准化后的基因型，βGRM是长度为M的向量，包含了SNP的随机效应，效应都从相同的正态分布中抽取，并且整体上服从协方差矩阵如下所示的多元正态分布，

这里BOlt-LMM为了避免近端污染（proximal contamination），采用了LOCO方法。

这个矩阵在习惯上称为GRM，或是亲缘关系矩阵K，于是有：

σg2是方差系数。环境效应也被认为是独立同分布，服从多元正态分布，

σe2是方差系数，I是单位矩阵。实际上σg2与σe2是未知的，所以我们要先通过REML来估计。然后计算前瞻性的卡方检验统计量：

其中，

使σg2与σe2为空模型：β=0是的估计值，在LOCO下，检验统计量变为：

BOLT-LMM-inf 无穷小混合模型统计量：

cinf是一个常数的校正因子，由下式估计：

使得，

实际操作中选取30个伪随机的SNP来估计cinf。我们可以将BOLT-LMM-inf统计量视为前瞻性统计量（将表型视为随机）的近似，或是回顾性的统计量（将基因型视为随机，基于SNP构建空模型）
BOLT-LMM 高斯混合模型关联统计量：
我们注意到，

是以下最优无偏估计（BLUP）的表型残差向量的标量倍数，

因此，BOLT-LMM-inf统计量就等价于计算（并调整）待检验的SNP xtest与BLUP残差的相关系数的平方。混合模型的power是基于以下事实，SNPs是基于对“去噪声”后的表型残差进行检验，即被混合模型估计的其他SNP的效应已经被矫正。我们可以一般化这个过程，定义：

其中 yresidual-LOCO表示拟合标准LMM的高斯混合扩展（用于待测SNP不在一条染色体上的SNP）后的一般化的表型残差向量，C表示校正因子，通过LD分数回归估计，以使得BOLT-LMM的卡方统计量回归后的截距匹配BOLT-LMM-inf的截距。在无穷小模型下，yresidual-LOCO与Vy成正比，BOLT-LMM的卡方统计量即为BOLT-LMM-inf的卡方统计量。
为了定义高斯混合模型LMM扩展，我们首先构建贝叶斯框架下的标准LMM模型，BOLT-LMM-inf的空模型是

其中，SNP效应βm（m是指除m号染色体之外染色体上的SNP）互相独立且服从以下的高斯先验分布

环境效应也互相独立，服从以下分布：

这里BLUP估计等同于计算遗传效应XLOCOβLOCO的后验均值

为了一般化这个模型（非无穷小模型），对于SNP效应，我们采用一个更一般化的先验分布，在BOLT-LMM中，使用了两个高斯分布的spike and slab的混合分布作为先验分布，如下所示：

这种混合更灵活的表示了遗传效应更为典型的长尾分布（heavier-tailed distributions）。在这个一般化的模型中，后验均值不再与BLUP相一致，但我们仍可以拟合这个贝叶斯模型以或得残差：

最后将残差带入前面的算式就可以得到BOLT-LMM 高斯混合模型关联统计量。

参考：

Loh, P. R. et al. Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nature Genetics 47, 284–290 (2015).

易感性尺度遗传力与观测尺度遗传力 Liability scale heritability & observed scale heritability

什么是易感性阈值模型？

参考：易感性-阈值模型 Genetic liability, Threshold model

什么是易感性尺度遗传力，以及观测尺度遗传力？

遗传力通常可以基于不能直接观测的易感性尺度（hl2），或是基于可观测的二分型表型（ho2）来计算。

通常遗传学家更为关注基于易感性尺度的遗传力（Liability scale heritability），主要原因是如果使用观测尺度遗传力（observed scale heritability），容易产生较大的偏差，原因有以下几点：

1 对于数量性状（ quantitative traits）来说，测量的尺度与遗传力的表现尺度是一致的（都是连续的），对于二分类性状来说（binary traits）, 病例或对照的状态 (case-control status) 是基于0 -1 尺度的，但遗传力在易感性尺度上才是容易解释的。

2 病例的确定。在病例对照研究中，通常病例所占的比例都要（远）高于人群中的流行率。但病例的确定通常会对遗传力的估计造成偏差。

如下图所示，A为数量变量的易感性分布，B二分类的形状在人群中（即随机）的易感性分布，C为病例对照试验中的易感性分布，刻意地过多纳入病例，会引起遗传力估计上的偏差。

3 SNP的质量控制（QC）。相比于数量性状的研究，病例对照实验的QC更为重要。对于数量性状来说，试验或测量上的误差一般不会与表型值相关，但病例对照实验中病例组与对照组一般都是独立采集的，所以试验误差容易造成病例与其他病例更为相似，对照也与其它对照更为相似。这样人工造成的误差会影响基于基因组相似性计算的遗传力。

如何转换？

详细推导过程可以参考下面这篇文章：

Lee SH, Wray NR, Goddard ME, Visscher PM. Estimating missing heritability for disease from genome-wide association studies. Am J Hum Genet. 2011;88(3):294-305. doi:10.1016/j.ajhg.2011.02.002

Lee SH 等人的文章介绍了转换的方法，当case和control并不是从人群中随机抽取的时候，转换公式如下：

hl2为 易感性尺度的遗传力 ，ho2为观测尺度遗传力

K为人群中病例的比例（流行率）

P为抽取的样本中病例的比例

z则为正态分布的密度函数的在所取阈值t处的值

使用R进行转换

#K = pop prevalence 人群中流行率
#P = proportion of cases in study 样本中病例比例
#h2 = Heritability estimate (on observed scale) 观测尺度遗传力
#T = liability threshold 易感性阈值
#zv = 正态分布的密度函数的在所取阈值t处的值

K=0.0659
P=0.0659
h2=0.0365
zv <- dnorm(qnorm(K))

h2_liab <- h2 * K^2 * ( 1 - K)^2 / P / (1-P) / zv^2
h2_liab

参考文献：

https://www.pnas.org/content/111/49/E5272

Estimating Missing Heritability for Disease from Genome-wide Association Studies

易感性-阈值模型 Genetic liability, Threshold model

易感性-阈值模型是遗传流行病学中重要的理论模型之一。

Liability 易感性

易感性是 遗传因素 与 环境因素 对某多因子疾病的效应的总称。因为易感性是一个隐变量（latent variable），实际上很难直接测量某个特定个体的易感性，但我们可以通过某群体中发病个体数量来估计该群体对于疾病的易感性。

Threshold Model 阈值模型

易感性-阈值模型（liability -threshold model）是我们用来分析非孟德尔遗传的（non-Mendelian）分类（categorical）表型（例如二分类表型 binary traits）的基本模型之一，如下图所示，通常我们认为易感性服从一个N(0,1)的正态分布。当某个个体的集聚的易感性超过了阈值T时就会发病，阴影区域的面积表述了在这个群体中该疾病的流行率（prevalence）。

对于某个疾病可以有多个阈值，分别对应疾病的不同严重程度。

参考：

https://onlinelibrary.wiley.com/doi/full/10.1002/0470011815.b2a05036